極限－余極限の例

２．２　余極限の抽象化

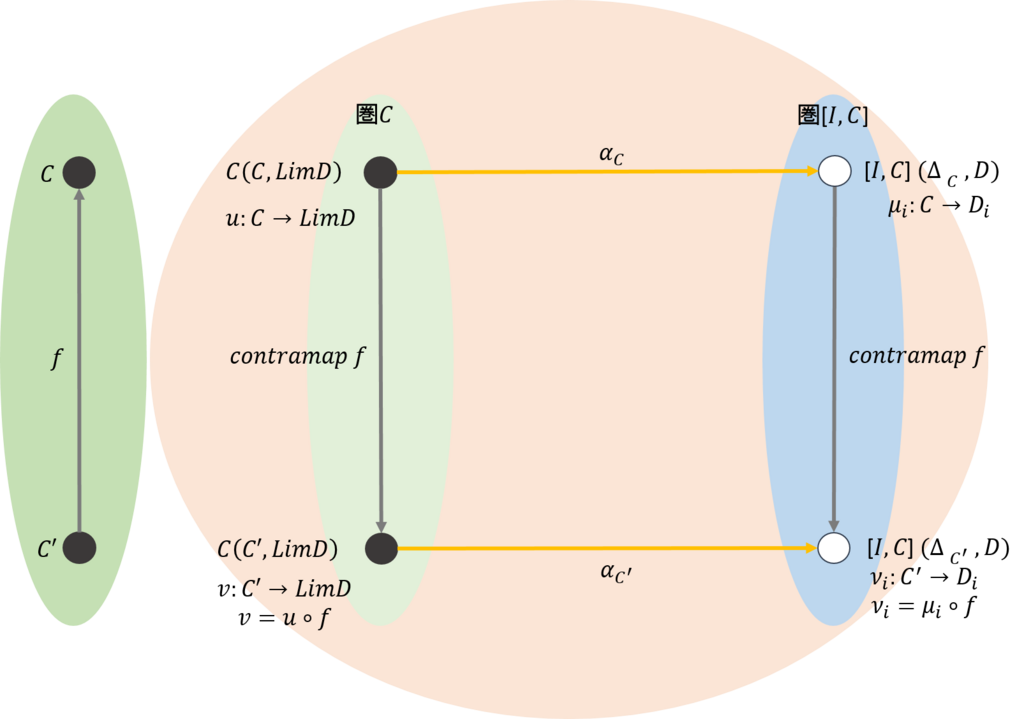
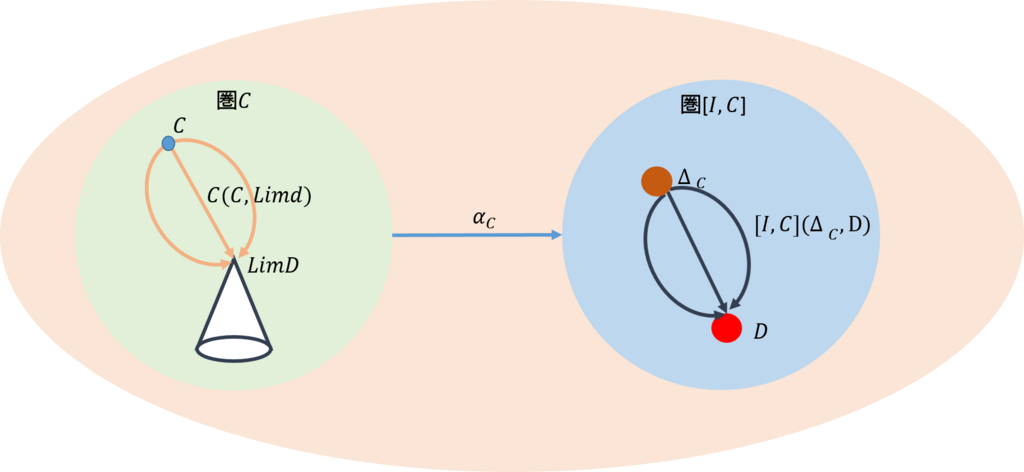
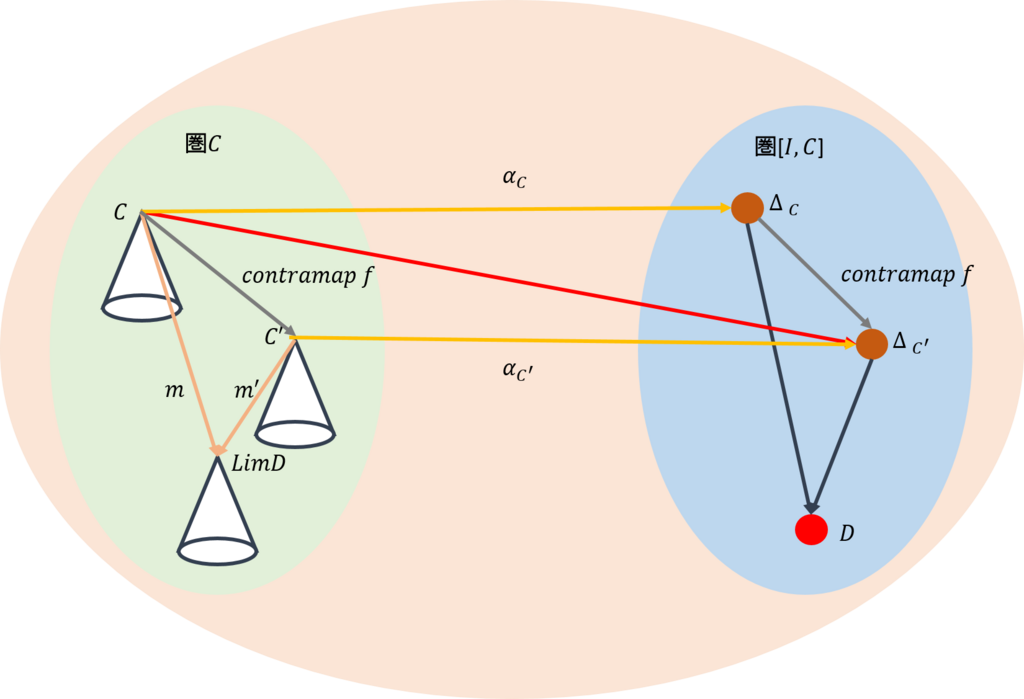
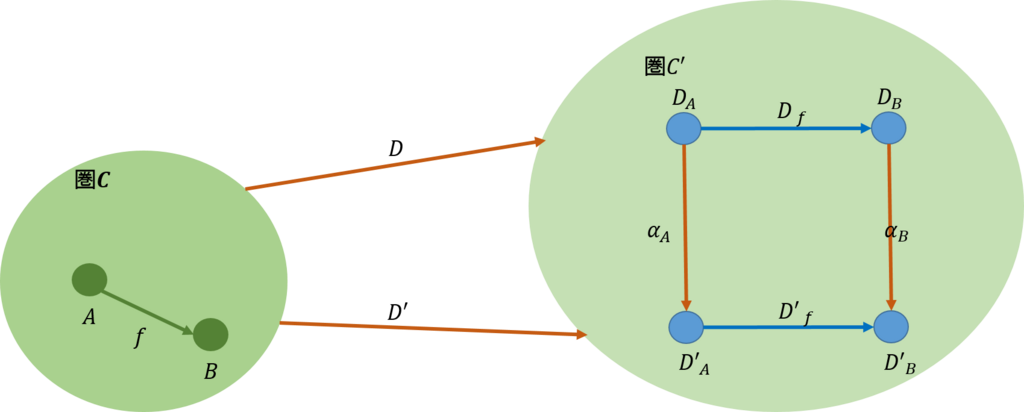
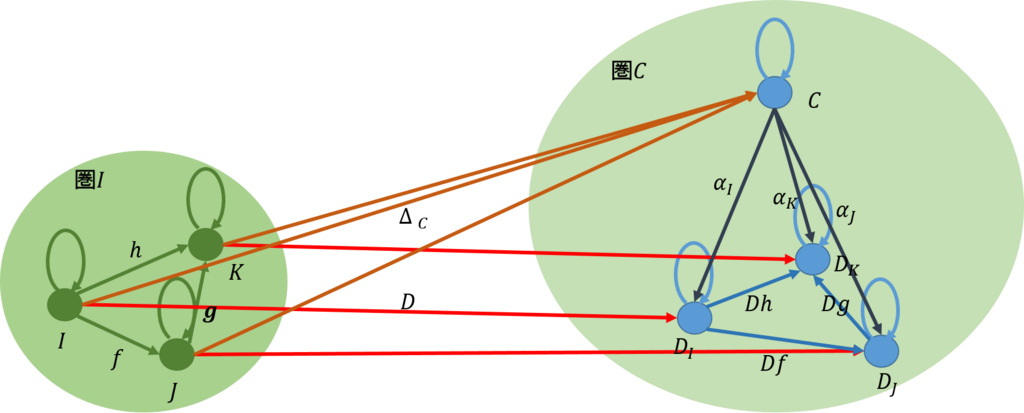
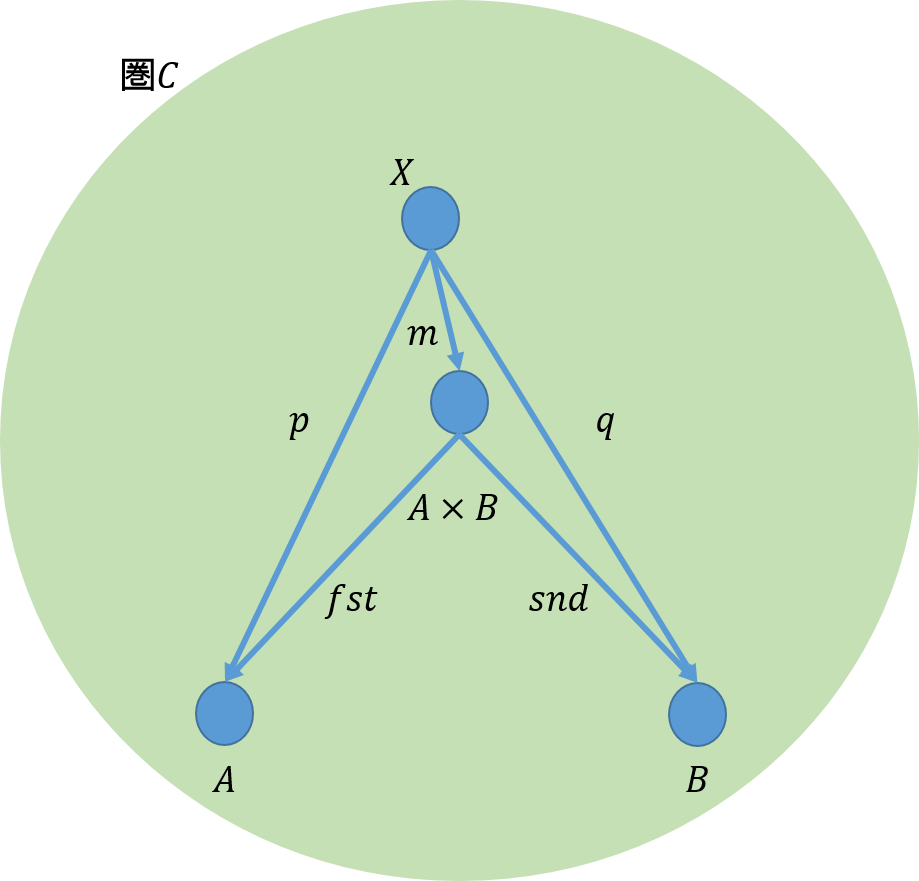
前回と同じように、余極限を抽象化してみよう。ここでは、下図のように、三つの圏を用意する。最初の圏\(\mathcal{C_0}\)は、余錐の頂点からなる圏だ。次の圏\(\mathcal{C}\)は余錐で構成される圏だ。最後の圏\([\mathcal{I,C}]\)はインデックス圏から余錐を構成したときの自然変換を射とする圏だ。

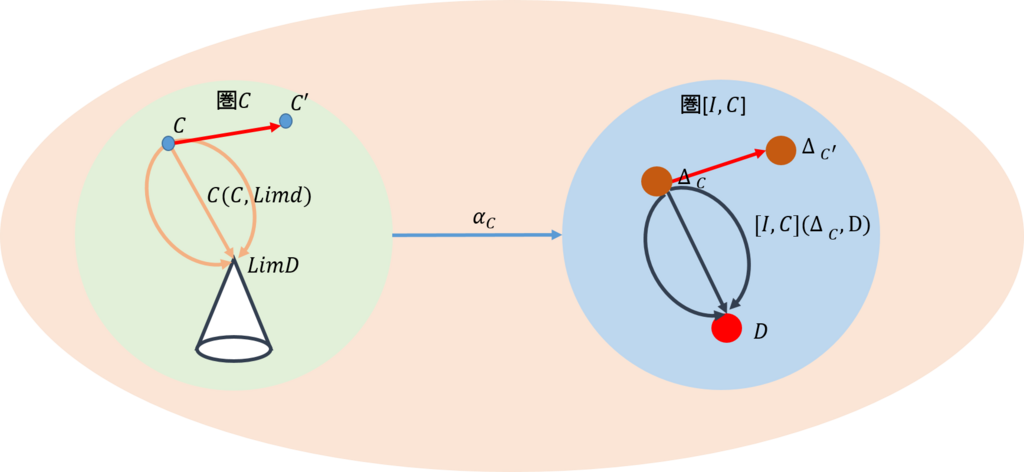
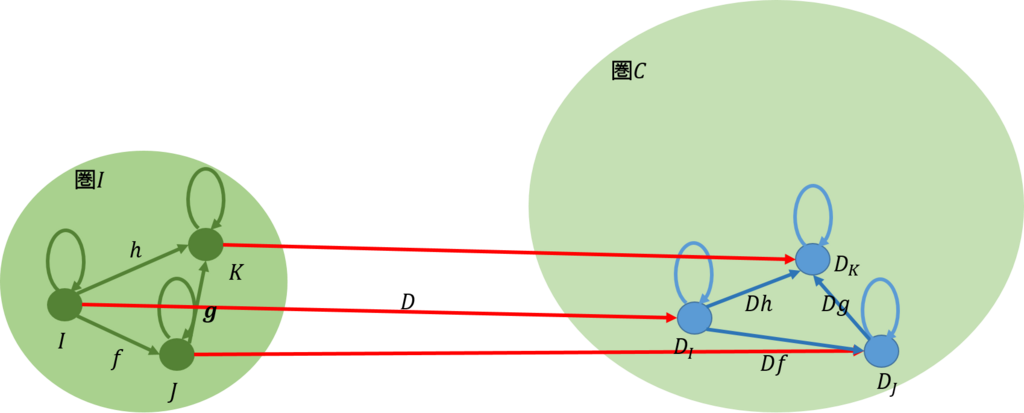
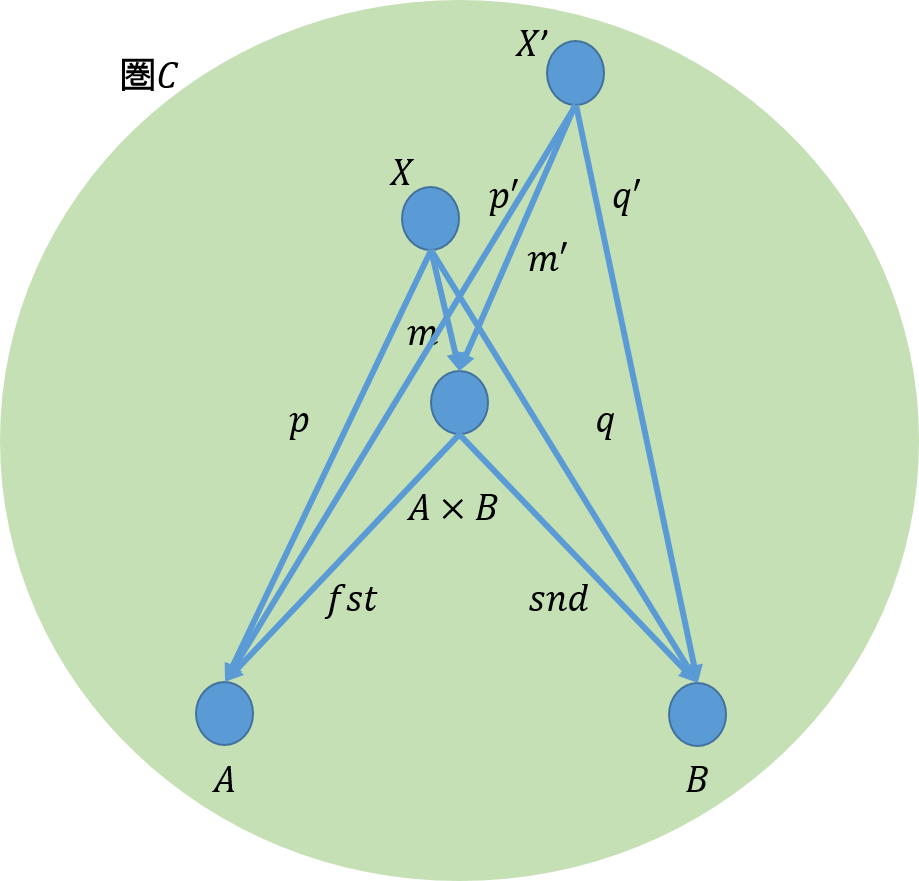
今、圏\(\mathcal{C_0}\)で、対象\(C,C’\)の間の射は\(f:C \rightarrow C’\)であったとする。圏\(\mathcal{C_0}\)から圏\(\mathcal{C}\)には、ある関手によって、上図の中ほどのように写されたとする。同様に、圏\(\mathcal{C_0}\)から圏\([\mathcal{I,C}]\)には上図の右側のように写されたとする。

前回と同じように、圏\(\mathcal{C}\)と圏\([\mathcal{I,C}]\)の間では上図のように可換が成り立つ。従って、圏\(\mathcal{C}\)で余錐を与えると、圏\([\mathcal{I,C}]\)からそれはどのような性格を有しているのかを得ることができる。

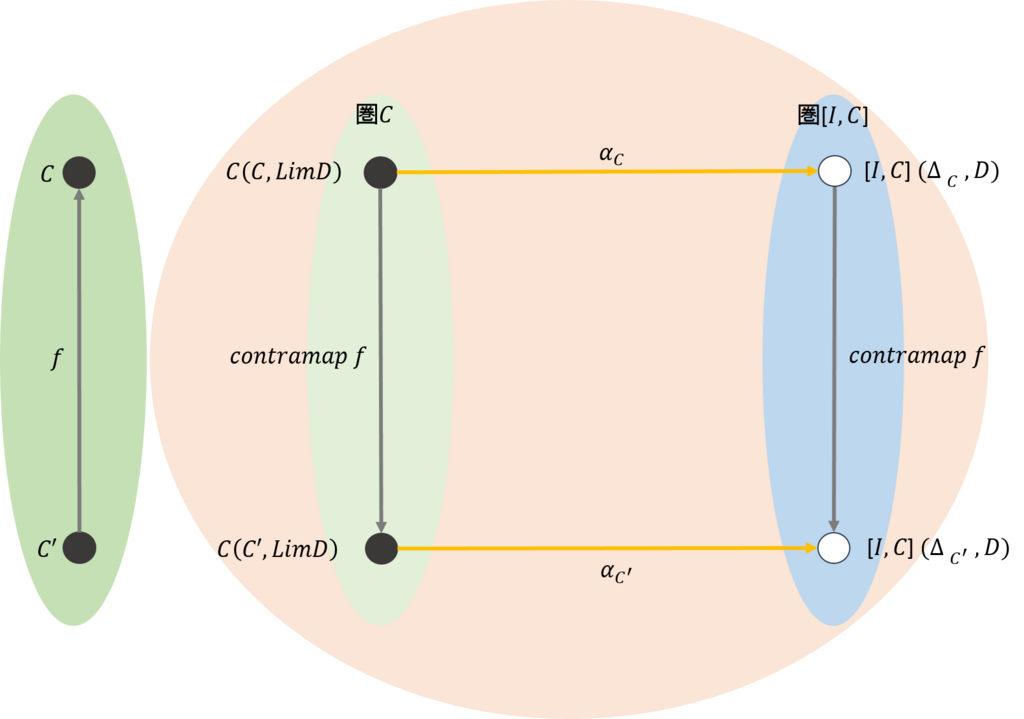
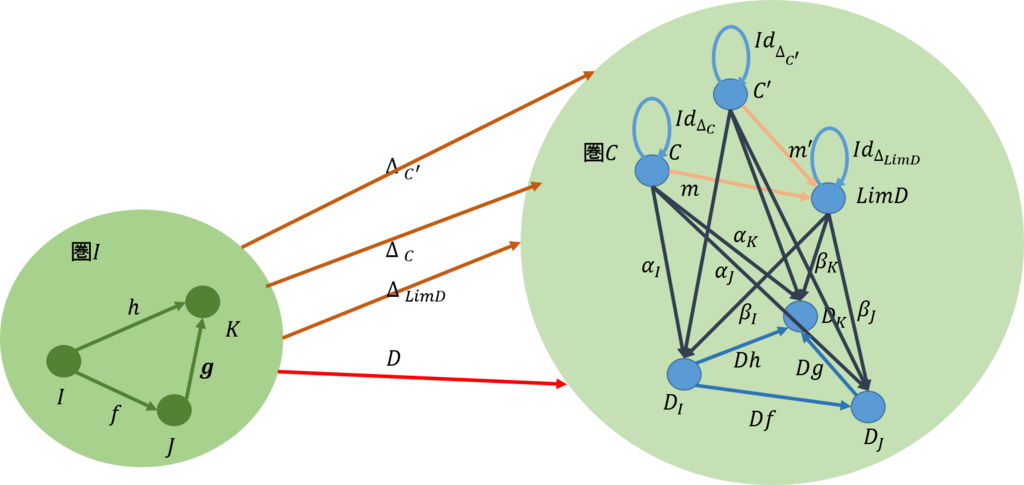
上の図は、下のような可換図式に書き換えることができる。

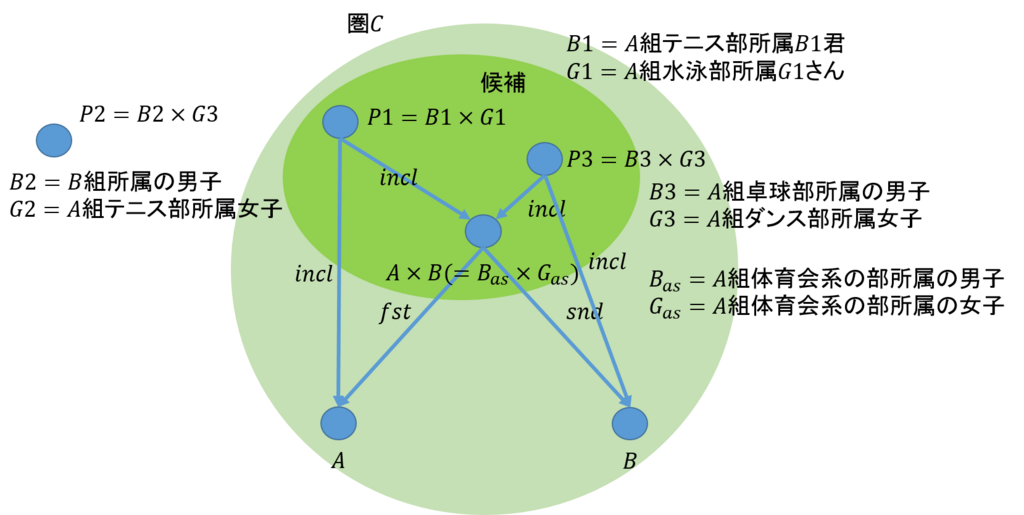
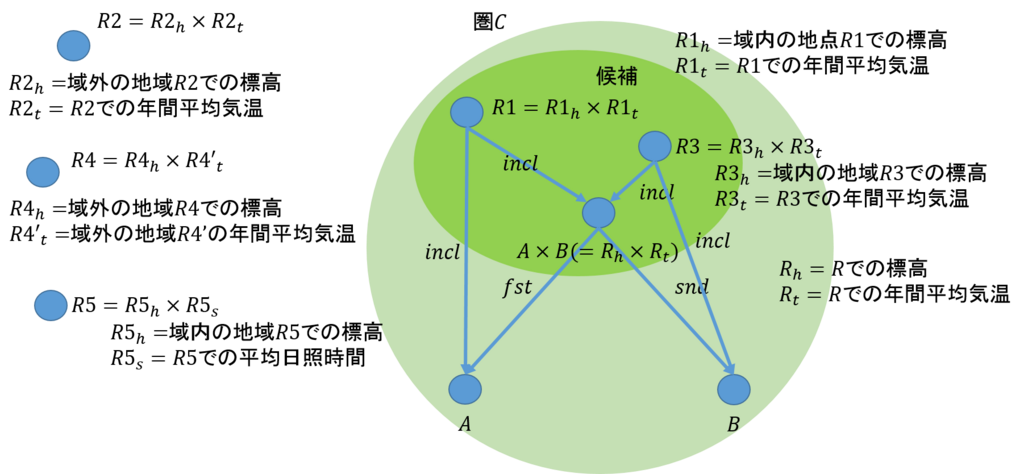
それでは、上の図を用いて、余極限のいくつかの例を挙げることにしよう。なお、例をあげるとき、対象\(C\)と余極限である対象\(ColimD\)とは一緒であるとする。

２．３　余極限の例

１）始対象

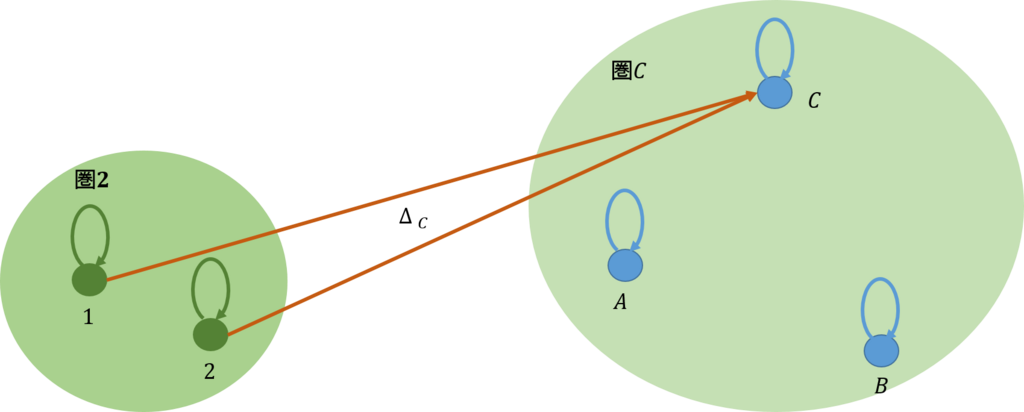
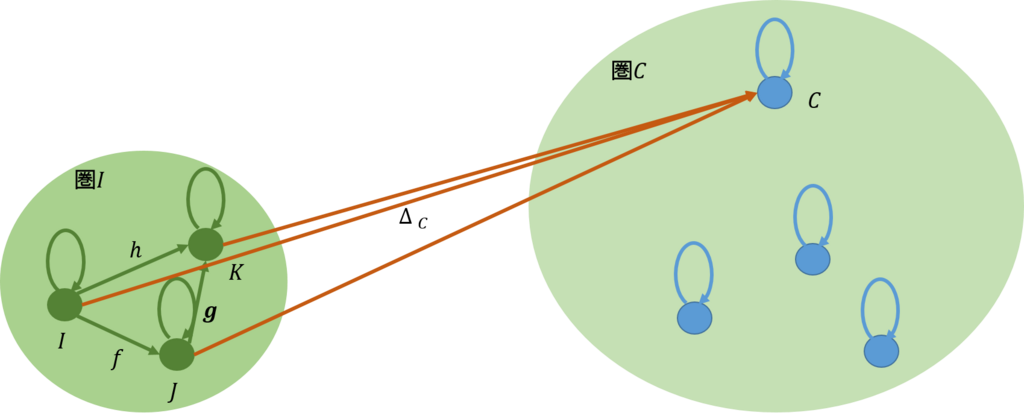
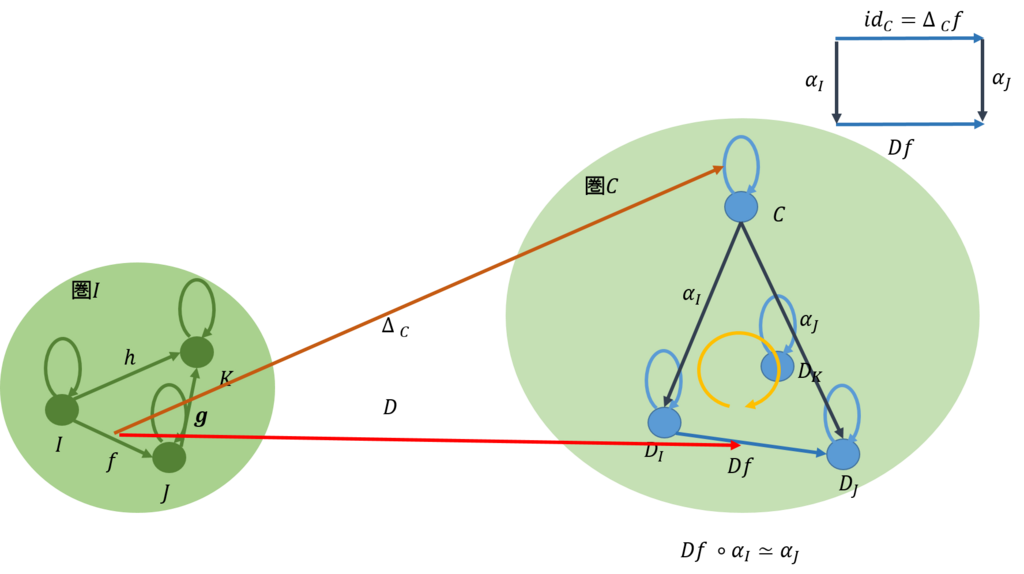
最初の例は、下図に示すように、余錐の上面が存在しない場合である。

上面が存在しないので、圏\(\mathcal{C}\)では余錐は頂点だけからなる。また、余極限の余錐\(C=ColimD\)から任意の余錐\(C’\)に対して、一意的に定まる射\(m’\)が存在する。これを、圏\([\mathcal{I,C}]\)に写すと下図のようになる。これから、関手\(\Delta_C\)から任意の関手\(\Delta_C’\)への射が一意的に定まることから関手\(\Delta_C\)が始対象であることが分かる。

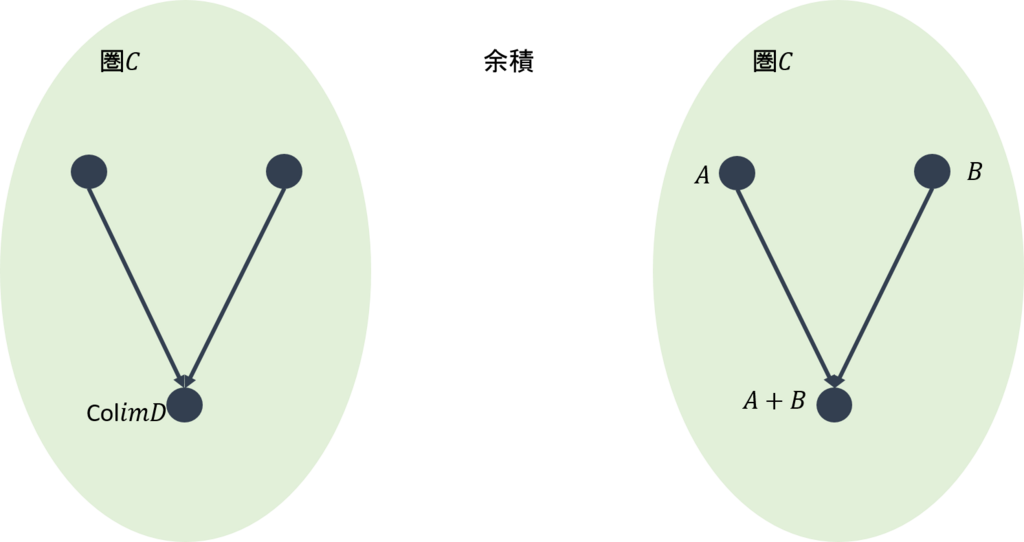
２）余積

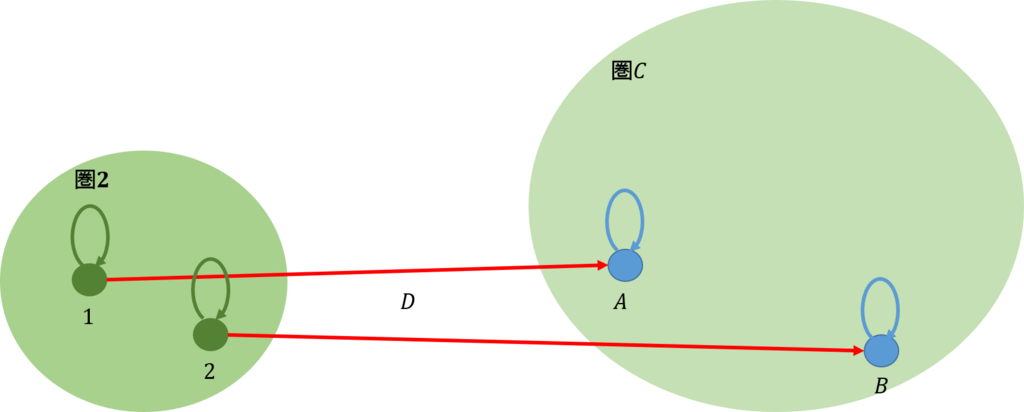
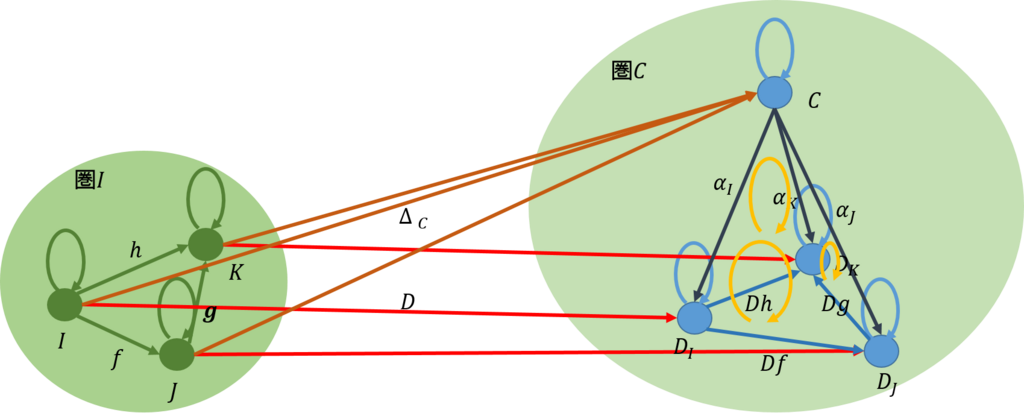
それでは、余錐が独立した
2頂点で構成されている場合を考えよう。下図のようになる。

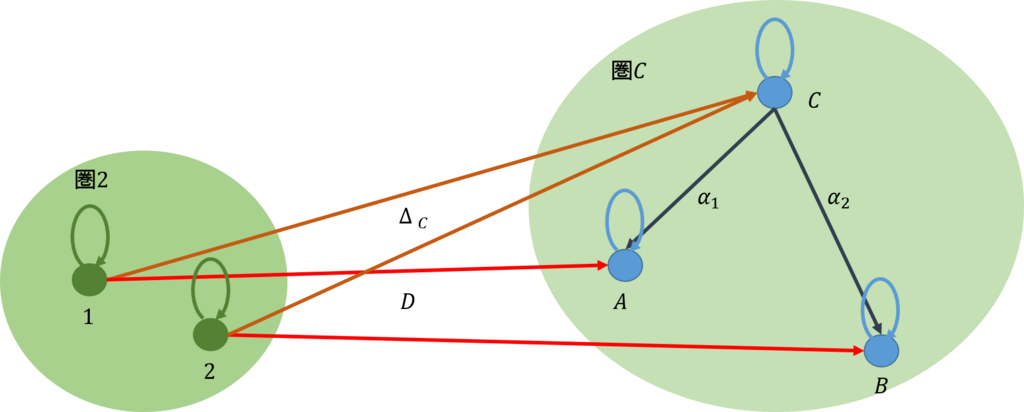
圏\(\mathcal{C}\)では、2頂点の余極限の余錐は上図の左側のようになる。これに、任意の余錐を加えたのが真ん中の図である。これを圏\([\mathcal{I,C}]\)に写したのが右図である。\(\Delta_C\)から\(\Delta_{C’}\)への射が一意的に定まることから、下図に示すように余積となる。

３）　コイコライザ

それでは、2頂点と、その間を同じ方向に二つの射が結んでいるような余錐について考えてみよう。下図のようになる。

錐の場合にはイコライザであったが、今回の場合はコイコライザになる。コイコライザの定義は次のようになっている。
「コイコライザの定義」適当な対象\(Q\)と射\(q:Y \rightarrow Q\)で\(q \circ f = q \circ g\)を満たすものが存在し、任意の対象\(Q’\)と射\(q’:Y \rightarrow Q’\)の組\((Q’,q’)\)で、\(q’ \circ f = q’ \circ g\)が与えられた時、射\(u:Q \rightarrow Q’\)が\(u \circ q=q’\)を満たすものが一意的に存在するとき、\((Q,q)\)の組をコイコライザという(下図参照)。

４）　押し出し

最後は上面の頂点が3個あり、一つから他の二つの頂点へ射が与えられている場合だ。これは下図のようになる。

これと双対の関係にあるものは、引き戻し(pullback)と呼ばれ、データベースを応用例として紹介した。
余極限の場合には、押し出し(pushout)と呼ばれ、共通のドメインを有する射の対が極限となる。

Puzzleと呼ばれるホームページに、押し出しを説明するのにちょうどよい例が上がっていたので、これを用いて説明しよう。

ホームページには、鹿なのだろうか、2匹の小動物が、角をくっつけあって遊んでいる木工パズルが紹介されている。

小動物をそれぞれ\(A,B\)、くっつけあっている部分を\(Z\)とすると、上図のパズルが完成した様子は\(A \cup_f B\)と記述することができる。ここで、\(\cup_f \)は\(Z\)の部分で接合しているという意味である。なお、もう少し正確に説明すると、\(Z\)は\(B\)の部分集合で、接合される部分である。\(f:Z \rightarrow A\)は\(A\)の接合部分を求める関数である。\(f(Z)\sim Z\)は\(f(Z)\)と\(Z\)が同値であることを示すもので、これにより、接合部分がくっつけられたことを意味する。

接合部\(Z\)は、\(A\)と\(B\)のぞれぞれの部分となっている。\(Z\)から\(A\)と\(B\)への射がこれを表している。また、\(A\)と\(B\)は、パズルが完成したときの構造物\(A \cup_f B\)の一部となっているので、それぞれから射が存在する。

上記で用いたのはattaching functionと呼ばれるものである。これが押し出しの例になるということを示したが、この関数についてさらに知りたい人は、WikipediaでAdjunction spaceを参照するとよい。

次の記事では、Haskellでの極限と余極限の利用例を示そう。

極限－余錐と余極限の定義

２．余極限

極限と双対の関係にあるのが、余極限である。

２．１　余錐と余極限の定義

前回までの記事で、極限について説明してきた。極限は錐(cone)を用いることで定義した。即ち、ある圏の中で錐が定義できたとする。そのような錐は、複数あっても一つでも構わないが、「どの錐からも一意的な射が存在するような錐が存在するとき、この錐を極限」と呼んだ。

双対は射の向きを反対にすることで得られる。極限の定理では、錐という専門用語を用いているが、余極限では、余錐(co-cone)という専門用語を用いる。錐は頂点(apex)から底面の方に向かって射が射影(projection)されていたのに対し、余錐は、底面の方から頂点に向かって射が射出(injection)される。余錐を用いると、余極限の定義は次のようになる。「どの余錐に対しても一意的な射が存在するような余錐が存在するとき、この余錐を余極限」と呼ぶことにしよう。

上記の言葉だけによる定義を、もう少し、明確にするために、インデックス圏を用いて定義することにしよう。下図のように、インデックス圏\(\mathcal{I}\)と圏\(\mathcal{C}\)が存在したとしよう。

インデックス圏は、説明を簡単にするために、3対象とそれらの間の射および恒等射で成り立っているとしよう(これは一般性を失うものではない。もっと多くの対象が存在したとしても、3対象に分割して考えられることによる)。

圏\(\mathcal{I}\)から圏\(\mathcal{C}\)への関手に設けることにしよう。一つは、圏\(\mathcal{I}\)の全ての対象\(I,J,K\)を圏\(\mathcal{C}\)の同一の対象\(C\)に移す関手\(\Delta_C\)としよう。この関手は、圏\(\mathcal{I}\)の全ての射\(f,g,h\)を圏\(\mathcal{C}\)の対象\(C\)の恒等射に写すことに注意しておこう。

もう一つは、圏\(\mathcal{I}\)の3対象\(I,J,K\)を圏\(\mathcal{C}\)の別々の対象\(D_I,D_J,D_K\)に写したもので、これを関手\(D\)としよう。このとき、圏\(\mathcal{I}\)の射\(f,g,h\)は圏\(\mathcal{C}\)の射\(Df,Dg,Dh\)に移されたものとする。

\(\bf{余錐の定義}\)
関手\(F\)から関手\(\Delta_C\)への自然変換が存在するとき、\(D_I,D_J,D_K\)を面とし、\(C\)を頂点としたものを、余錐と呼ぶことにする。なお、錐の場合には、頂点を上に描いたが、余錐の場合には、頂点を下に描くことにする。従って、\(D_I,D_J,D_K\)によって作られる面は上に来るので、余錐の上面と呼ぶこととする。

\(F\)と\(\Delta_C\)による自然変換が存在するとは、上図では、
\begin{eqnarray}
\alpha_I = \alpha_J \circ Df \\
\alpha_J = \alpha_K \circ Dg \\
\alpha_I = \alpha_K \circ Dh
\end{eqnarray}
が成り立つことである。

\(\bf{余極限の定義}\)
圏\(\mathcal{C}\)内の任意の余錐に対して、ある余錐から一意的に定まる射が存在するとき、この余錐を余極限(colimit)と呼ぶ。

次の記事では、余錐の例を挙げるための準備をしよう。

極限－極限の例

１．８　錐の例

今年のブログの締めは、少しでも圏論が身近に感じられるようにするために、錐の例を取り上げよう。

前回のブログで、抽象度の高い、下図のような極限の可換図式を示した。

この可換図式は、錐を作成すると、それがどのような極限なのかを、示してくれる。

上図で、圏\(C\)は、対象となっているのは錐だけで、射となっているのは錐の頂点間の写像という極めて簡素な圏である。

圏\([\mathcal{I,C}]\)はインデックス圏\(I\)から圏\(C\)への関手によって、錐がどのような構造を持っているかを示した圏である。

それでは、いくつかの例を示そう。

１）終対象

最初は、底面のない錐である。圏\(\mathcal{C}\)があった時、その対象は底面のない錐であったとしよう。その中には、極限と呼ばれる錐\(C’\)が存在する。これを\(LimD\)と記述しよう。これを下図の左側に示す。

そして、圏\(\mathcal{C}\)から任意の対象\(C\)を取り出そう。\(C\)も\(C’(=LimD)\)も錐であり、そして、\(C’\)は極限の錐であることから、\(m:C \rightarrow C’\)となる一意に定まる関数が存在する。そして、\(f:C’ \rightarrow C\)とした時、\(m= contramap \ f\)となる。これらの関係を下図の真ん中に示す。
これらの関係については、下図を参照のこと。錐の頂点は正確に記述すると\(\mathcal{C}(C',LimD)\),\(\mathcal{C}(C,LimD)\)だが、ここでは、簡略して\(C',C\)と記述している。

これを圏\([\mathcal{I,C}]\)に移すと、下図の右側の図となる。これは、任意の対象について成り立っていることから、任意の対象\(\Delta_C\)から\(\Delta_{LimD}\)への射\(contramap \ f\)が存在することとなり、\(\Delta_{LimD}\)は終対象となる(なお、\(contramap \ f \)は圏\(\mathcal{C}\)と圏\([\mathcal{I,C}]\)で同一に記述しているが、構造は似ているものの異なる関数であることに注意しておこう)。

従って、頂点だけの錐は、極限が終対象となることが分かる。

２）積、デカルト積、冪

次の例を示そう。次の圏\(C\)は、底面は有するが、2頂点だけで、辺を持たない錐を対象にしているものとする。それを、下図の右側に示す。

前回の例と同じように、錐\(C,C’\)を定めることにしよう。\(C’=limD\)は極限の錐である。これを示したのが、下図の左側と真ん中である。

そして、これを圏\([\mathcal{I,C}]\)に移してみよう。これは、圏\(\mathcal{C}\)の積であることが分かる。

もう少し、分かりやすく示したのが下図である。

底辺の頂点をさらに具体的にすると下図のようになる。底辺の頂点\(A,B\)が集合である時は、下図の右側に示すように、錐の頂点\(A \times B\)はデカルト積\((A,B)\)となる。

また、底辺の頂点\(X,Y\)を写像のドメインとコドメインと考えると、\(X \times Y\)は定数関数となり、冪\(Y^X\)で表される。(なお、\(X\)から\(Y\)への写像は、\(X\)の集合の要素の数を\(X\)とし、\(Y\)の集合の要素の数を\(Y\)とすると、定数関数の数は、\(Y^X\)となる。これを利用して、関数をこのように冪を用いて表現している)。

３）イコライザ

さらに、例を示そう。次の圏\(C\)は底面に2頂点を有し、一方の頂点から他方の頂点へ二つの射\(f,g\)があるものとする。これを、下図の右側に示す。

前回の例と同じように、錐\(C,C’\)を定めることにしよう。\(C’=limD\)は極限の錐である。これを示したのが、下図の左側と真ん中である。


これを、圏\([\mathcal{I,C}]\)に移すと上図の左側の図になる。

かつて、イコライザの説明をした時に、これを次のように定義した。

「イコライザの定義」適当な対象\(E\)と射\(eq:E \rightarrow X\)で\(f \circ eq = g \circ eq\)を満たすものの組\((E,eq)\)が存在し、任意の対象\(O\)と射\(m:O \rightarrow X\)の組\((O,m)\)で、\(f \circ m = g \circ m\)が与えられた時、射\(u:O \rightarrow E\)が\(eq \circ u = m\)を満たすものが一意的に存在するとき、\((E,eq)\)をイコライザという。

下図に示すように、圏\([\mathcal{I,C}]\)はイコライザの定義そのものである。従って、底辺の2頂点間で同一方向に二つの射が存在するとき、極限はイコライザとなる。

４）引き戻し

さらに、例を示そう。次の圏\(C\)は底面に3頂点を有し、二つの頂点から残りの一つの頂点への写像が存在するものである。それを下図の右側に示す。


この例はデータベースである。具体的に示そう。ある学年の名簿を作成したと仮定しよう。そして、上の図に示すように、錐の頂点はデータベースという対象である。ここには、男子学生、女子学生、組のテーブルがある。男子学生のテーブルには、名前を記載するフィールドと所属する組を示すフィールドがある。女子学生のテーブルも同じである。また、組のテーブルは、クラスの名前を記入する。

データベースからの射が、男子学生、女子学生、クラスと呼ばれる集合で、これらは錐の底辺での頂点となる。そして、頂点間では、男子学生と女子学生からクラスへの射が設けられている。

ここで、射の方向を変えて、クラスの側から男子学生あるいは女子学生を観察したらどのようになるであろうか。例えば、A組に属している男子学生を求めたとしたら、それは、{太郎、次郎、…}というように構成員の集まりとなる。通常、写像はコドメインとなっている集合の要素を与えてくれるが、この場合は、集合を与えてくれる。

このような場合、上図に示すように、男子学生からクラスへの写像の値が一致する男子学生の集合を表すために一本の線を引き、その線上に構成要素を記述する。これは、数学の用語では、ファイバーと呼んでいる。ホモトピーなどを学ぶときなどに、必要とされる概念である。

また、この錐の極限を、引き戻し、あるいはファイバー積という。

宿題：上記のデータベースを極限を用いてHaskellで実現しなさい。

年が明けたら、極限と双対関係にある、余極限について説明する。それでは、良いお年をお迎えください。

ジューシーなターキーをクリスマスに楽しむ

昨年、ブライン液に浸して、ジューシーなターキーを食べることができたので、今年も、これを利用することにした。ただし、昨年は、塩だけしか利用しなかった。砂糖も一緒に用いるとよいという情報も得ていたが、甘くなるのも嫌だなと思い、塩だけでブライン液を作った。

しかし、最近になって、砂糖を用いると水分がより吸収されるという記事を見たので、昨年とは異なるブライン液を作ることにした。

今年も昨年と同じ大きさのミニ・ターキーを仕入れた。

成城石井に電話をして、確保したのが、このターキーである。お店の方で解凍してくれたので、料理する前の日まで冷蔵庫に保存しておき、最終の夜は冷たい家事室に移した。

今年も、孫たちが23日が都合がよいというので、イブのイブにターキーを食べることにした。朝8時から、ブライン液を作り始めた。水3リットルに対して、塩と砂糖をそれぞれ150g加えた。

バケツの中にビニール袋を二重にし、その中に、水、塩、砂糖を注入した。

ターキーを袋から取り出すと、水が大量にこぼれる。これらの水は、本来、ターキーの中にあったものが、解凍に伴って流れ出てきたものだろう。ターキーの肉をぱさぱさにさせる要因だ。ターキーの重さを量ったら2.9Kgであった。

これをブライン液の中に4時間ほど浸した。


昼食後、ローストの作業に取り組んだ。ローストに使う材料は、以下の通りだ。

ターキーに使う野菜は、臭い消しと出汁が主なので、手ごろな野菜を利用するのだが、今年はどの野菜も高く、屑野菜を用いたという気分にはならなかった。
野菜は、セロリ、ニンジン、キャベツ、玉ねぎ、パセリ、ローズマリーだ。さらに、ジャガイモを一緒に蒸かすことにした。

野菜を細かく切って、オーブン皿にもる(ジャガイモの姿も見えるが、これは、取り出して、後から、オーブンの中に入れた)。

ブライン液から取り出したターキーはこのような感じ。

重さをはかってみたら、3.0Kgであった。水分100gを吸ったことになる。昨年は、ブライン液の変化で吸われた水分の量を推定したが、正確ではなかったと思う。今年のほうが正しい量だ。
冷蔵庫に栗の瓶詰があったので、ターキーの内臓に栗を詰めた。
ターキーは、全身を塩胡椒して、オーブン皿にのせた。内臓から取り出した、首と砂肝も一緒にのせた。

ターキーの上には、一箱のバターを手ごろな大きさに切ってのせた。

オーブンを250度にし10分ほど焼いた。その後、温度を下げて焼く。低温の方がおいしく焼けるという記事を読んだので、去年より10度低くして、170度にした。ポップアップタイマー(写真の真ん中右上にある赤いもの)が上がってくるまで焼いた。これには、1時間40分要した。その間、20分おきぐらいに煮汁をターキーの上にかけた。なお、ジャガイモは、焼きすぎを避けるため、ターキーを焼き始めてから30分後にオーブン皿に加えた。

焼き上がりはこのような感じ。

煮汁を利用して、ターキーにかけるスープを作る。濾した煮汁を鍋に移し、ローリエ一枚とマギーブイヨン一粒をくわえ、煮立ったところで、ウィスキー大匙一杯を加え、アルコールを飛ばして出来上がりだ。

サラダやコーンスープやワインなどと一緒に、孫たちと一緒に5人で食した。


ブライン液から出した後、ターキーは水洗いをしないで、そのまま用いたので、砂糖の甘みが心配であったが、だれも気にしなかった。
孫たちは成長期ということもあり、あっという間に食べられてしまったが、ジューシーで、とても美味しいターキーだった。

極限－錐と極限のさらなる抽象化

１．７　錐と極限のさらなる抽象化

前回の記事で、錐は二つの異なる方法で作成できることが分かった。一つは、錐の頂点から錐の底面への写像を自然変換で与えるものである。もう一つは、求める錐の頂点から極限の錐の頂点への射を与えるものである。

前回は、さらに、この二つの方法は同型の写像を与えることも示した。写像が同型であるので、この間で自然変換を定義できるようになる。求める錐の頂点を\(C\)としたとき、この始自然変換を\(\alpha_C\)で表すことにしよう。図で示すと次のようになる。

ここまでが前回の話である。

それでは、この方法によって、\(C\)を頂点とする錐が得られたとする。この得られた錐から、別の錐\(C’\)を求めるにはどのようにしたらよいであろうか(下図)。

なお、\(C\)と\(C’\)には、\(f:C’ \rightarrow C\)の関係があるものとする。ここで、\(f:C \rightarrow C’\)でないことに注意しておいてほしい。訳はすぐに分かる。

これの可換図式を求めると次のようになる。なお、関手は射も写像するが、その時移す側と移される側で向きが同じとき、この関手は共変関手(contravariant)と呼ばれる。それに対して、反対になるときは、関手は反変関手(contravariant)と呼ばれる。そこで、上の図では反変関手なので、\(f\)が移されている先を\(contramap \ f\)とした。

上図の可換図式で\(\mathcal{C}(C,LimD)\)は射の集合であるので、それを\(u: C \rightarrow LimD\)と表すことができる。また、\(\mathcal{C}(C’,LimD)\)を\(v: C' \rightarrow LimD\)と表すことができる。ところで、\(f:C' \rightarrow C\)なので、\(v=u \circ f\)となる。

また、\([\mathcal{I,C}](\Delta_C,D)\)は自然変換である。従って、これはインデックス圏の対象\(I\)毎に、\(\mu_I:C \rightarrow D_I\)と表すことができる。同様に、\([\mathcal{I,C}](\Delta_{C'},D)\)を\(\nu_I:C’ \rightarrow D_I\)と表すことができ、先ほどと同様に、\(\nu_I =\mu_I \circ f\)となる。

この関係を示したのが下図である。

この可換図式から、圏\(\mathcal{C}\)での頂点を\(C\)とする錐から、圏\([\mathcal{I,C}]\)での頂点\(C’\)の錐を求めるには、圏\(\mathcal{C}\)で\(C’\)に移動してから圏\([\mathcal{I,C}]\)にジャンプしてもよいし、圏\(\mathcal{C}\)から圏\([\mathcal{I,C}]\)にジャンプしてから\(C’\)に移動してもよいと言っている。これを図で表すと以下のようになる。

極限の理論的な話はここまでだが、次回はいくつか例を示そう。

極限－錐と極限の抽象化

１．６　錐と極限の抽象化

前回の記事までで、インデックス圏を用いての粋と極限の求め方を説明してきた。その中では、インデックス圏から粋を作成しようとしている圏へ、三角形のまま移す関手と、一点にまとめる関手を用意した。前者は錐の底辺を形成し、後者は錐の頂点を形成することも説明した。また、インデクス圏に用意するものは三角形に限る必要はなく、多角形でもよいこと、さらには、それを無限とした円でもよいことを説明した。また、錐を構成するする条件として、全ての側面で可換であるということも説明した。

それでは、このようにして出来上がった錐をもう少し抽象化した件の中で考えることにしよう。

抽象化１

錐を作成するとき、インデックス圏\(\mathcal{I}\)と錐を構成する圏\(\mathcal{C}\)を用意し、その間を関手\(C,\Delta_C\)で結んだ。また、関手間に自然変換\(\alpha\)を定義した。

そこで、関手を対象とし、自然変換を射とすることで、新たな圏を定義することができる。これを圏\([\mathcal{I,C}]\)と呼ぶことにしよう。

抽象化2

もう一つは極限の錐を利用するものだ。圏\(\mathcal{C}\)の中に作られた錐を対象とし、それぞれの錐の頂点から極限の錐の頂点への写像を射とするものだ。これをそのまま圏\(\mathcal{C}\)としよう。ただ、それぞれの錐では、その側面が可換になっているということに注意しておこう。

この二つの抽象化を図で表すと次のようになる。


直感的にこの二つは、同じであると感じであろう。左の方は、関手\(\Delta_C\)と\(D\)が与えられると、錐が形成されると説明している。右の方は、極限の錐の頂点\(LimD\)が与えられているとする。そして、ある対象\(C\)から極限の錐の頂点への射\(m\)が与えられたとき、その対象\(C\)は、錐の頂点になると言っている。従って、両方とも同じことを言っている。そこで、これをもう少し厳密にして、定理として示すことにしよう。

二つの抽象化は同型である

上の図を一般化して、下図のようにする。

まず左側について説明する。\(\Delta_C\)と\(D\)の間の自然変換は、一般には、一つとは限らず複数となる場合もあり、集合となる。そこで、これを\([\mathcal{I,C}](\Delta_C,D)\)としよう。なお、自然変換がない場合もあるが、この場合には、錐を構成できないということになる。

次に右側を説明する。対象\(C\)から極限の錐の頂点\(LimD\)への射も、同じように一つとは限らず複数存在する場合もある(無の場合もあるが、この場合には錐を構成できないということになる)。この集合を\(\mathcal{C}(C,LimD)\)としよう。なお、\(C\)については錐であるという条件を課する必要はない。これは、後で分かるが、射がある場合には、必然的に、錐となる。

それでは、右側と左側は同型であることを示すこととしよう。

1) まず、左側から右側が導かれることを示す。これは、\([\mathcal{I,C}](\Delta_C,D)\)ならば\(C\)から\(LimD\)への射があることを示せばよい。

これは簡単である。関手\(\Delta_C\)と\(D\)によって錐を作成したとすると、その錐の頂点から極限の錐の頂点へ射\(m\)が存在することは、極限の錐の定義から明らかである。従って、\(m \in (\mathcal{C}(C,LimD)\)となるので、証明できたこととなる。

2) 次に、右側から左側が導かれることを示す。\(\mathcal{C}(C,LimD)\)であるならば、\([\mathcal{I,C}](\Delta_C,D)\)であることを示せばよい。

これには、射の集合\(\mathcal{C}[C,Limd]\)から任意の一つの射を取り出す。これを\(m\)としよう。このとき、\(C\)を頂点とする錐が構成できれば、証明できたことになる。これは、錐の辺が構成されることを、元々のインデックス圏の対象ごとに示せばよい。

下図に示すように、インデックス圏の対象\(I\)について考えてみよう。極限の錐にはその定義から射\(\beta_I\)が存在する。従って、\(m\)と\(\beta_I\)を合成したものは、射となるので、これを\(\alpha_I\)とする。これは、とりもなおさず、\(C\)を頂点とする錐の辺である。全てのインデックスの対象に対して、上記の操作を施すことで、\(C\)を頂点とした錐を実現することができ、証明は終わりである。

極限－極限の定義

１．５　極限の定義

前回の記事で、インデックス圏から錐を作成する方法を示した。

上図で、関手\(D\)によって、インデックス圏\(\mathcal{I}\)での三角形(頂点が対象、辺が射)が、圏\(\mathcal{C}\)に移され、これから作成される(三角)錐の底辺を形成する。この底辺の各頂点は\(\mathcal{I}\)の対象を、また、各辺は\(\mathcal{I}\)の射を、関手\(D\)によって、それぞれ移したものである。

また、上の図で、圏\(\mathcal{I}\)の三角形の頂点、即ち、対象の全てを、関手\(\Delta_C\)によって、一つの対象\(C\)に移した。このとき、圏\(\mathcal{I}\)の三角形の辺、即ち、射の全ては、\(\Delta_C\)によって、\(C\)での恒等射\(Id_{\Delta_C}\)に移される。

関手\(\Delta_C\)と関手\(D\)の間で、自然変換\(\alpha=\{\alpha_I,\alpha_J,\alpha_K\}\)が存在するなら、三角錐\(C,D_I,D_J,D_K\)が構成され、その側面は可換となっている。即ち、\(Df \circ \alpha_I = \alpha_J\), \(Dg \circ \alpha_J = \alpha_K\),\(Dh \circ \alpha_I = \alpha_K\)である。

同様に、関手\(\Delta_C’\)からも同じように側面が可換となっている三角錐を構成できる。

このような三角錐がいくつもできるであろう。その中で、極限と呼ばれるものを定義することにしよう。得られた三角錐の中から一つの頂点を選び、これを\(LimD\)と呼ぶことにしよう。\(LimD\)を頂点とする三角錐が次の条件を満たす時、極限という。なお、この三角錐での自然変換を\(\beta=\{\beta_I,\beta_J,\beta_K\}\)とする。

[条件] 任意の(三角)錐の頂点\(C\)に対して
1.　一意的に定まる射\(m: C \rightarrow LimD \)が存在し、
2.　圏\(\mathcal{I}\)の全ての対象\(i\)に対して、\(\beta_I \circ m = \alpha_I\)となる。即ち、上記の図の場合には、\(\beta_I \circ m = \alpha_I\),\(\beta_J \circ m = \alpha_J\),\(\beta_K \circ m = \alpha_K\)である。

説明では、理解しやすくするために、インデックス圏を三角形としたが、多角形でも構わない。さらには、辺の数が無限となった円でも構わない。

なお、このような射\(m\)は分解射(factorization)と呼ばれる。

また、\(\beta_I,\beta_J,\beta_K\)は、専門用語を用いれば、モノ射である。モノ射は次のように定義されている。射\(f:X \rightarrow Y\)がモノであるとは、任意の射\(g_1,g_2:Z \rightarrow X\)に対して、\(f \circ g_1= f \circ g_2\)であるならば、\(g_1=g_2\)が成り立つ。

極限－錐

１．４　錐

これまで、2回にわたって、圏論での極限の具体的な例を示してきた。そこでは、二つの対象\(A\),\(B\)とその極限\(A \times B\)ということで説明をした。また、極限は、ある条件を満たすものの中で最も良いものといういい方もした。また、ある条件を満たすものを候補とも説明した。

それでは、このような候補はどのようにして選ばれるのであろうか。あるいはさらに戻って、二つの対象はどのようにして選ばれるのであろうか。これらを選ぶ基準がないと、極限という概念を組み立てていくことができない。

そこで、ここでは、これらの選び方について説明することとする。

2対象からの錐

まず単純な例から説明しよう。二つの圏が与えられているとする。

一つの圏は、二つの対象\(1\),\(2\)しか有しない離散的な圏としよう(下図)。即ち、射は恒等射\(id\)しか有しないものとしよう。これを圏\(\bf{2}\)と呼ぶことにしよう。

もう一つの圏を\(\mathcal {C}\)と呼ぶことにし、ここから二つの対象を適当に選び、これを\(A\),\(B\)にしたとしよう。そこで、圏\(\bf{2}\)からこれらの対象に関手\(D\)を張ることを考えよう。これは、
\begin{eqnarray}
A=D(1) \\
B=D(2) \\
id_A=D(id_1) \\
id_B=D(id_2)
\end{eqnarray}
となるような\(D\)が存在するならば、関手を張ることが可能である。ここで、\(id_1,id_2,id_A,id_B\)はそれぞれの対象での恒等射である。

このような関手が張れたとしよう(上図)。そして、\(\mathcal {C}\)からもう一つ対象を選んできたとし、これを\(C\)としよう。これに対して、圏\(\bf{2}\)からこの対象に関手\(\Delta_C\)を張ることを考えよう。同じように
\begin{eqnarray}
C=\Delta_C (1) \\
C=\Delta_C (2) \\
id_{C}=\Delta_C (id_1) \\
id_{C}=\Delta_C (id_2)
\end{eqnarray}
となるような\(C\)が存在するならば、関手を張ることが可能である。ここでも満たしたとしよう(下図)。

そこで、\(D\)から\(id_{C}\)への自然変換を考えよう。

自然変換

それでは、自然変換を復習しておこう。

下図に示すように、圏\(\mathcal{C}\)から圏\(\mathcal{C'}\)に対して関手\(D,D'\)が存在したとしよう。

関手\(D\)から\(D'\)への自然変換\(Nat(D,D')\)とは、\(\mathcal{C}\)の任意の対象\(A,B\)に対して、上図が可換になることを言う。なお、\(A\)から\(B\)への射を\(f:A \rightarrow B\)とする。

上図は次のようになっている。
\begin{eqnarray}
D_A = D (A) \\
D_B = D (B) \\
D_f = D (f) \\
D'_A = D' (A) \\
D'_B = D' (B) \\
D'_f = D' (f)
\end{eqnarray}
である。

従って、可換は、\(\alpha_B \circ D_f ＝ D'_f \circ \alpha_A\)を満たすこととなる。

圏\(\bf{2}\)からの自然変換

それでは、圏\(\bf{2}\)の自然変換を考えてみよう。(下図)。

例えば、圏\(\bf{2}\)での対象1について考えよう。これは、\(D\)によって\(A\)に、\(\Delta_C\)によって\(C\)に写像変換されている。\(C\)から\(A\)への写像を\(\alpha_1\)とすると、これが自然変換を構成する要素となる。

対象2についても同様で、\(C\)から\(B\)への写像を\(\alpha_2\)とすると、これが自然変換を構成する要素となる。

なお、\(A\)と\(B\)の間には写像が存在しないので、可換の条件は存在しない。このため、\((\alpha_1,\alpha_2)\)は自然変換\(Nat(\Delta_C,D)\)となる。
一般には、自然変換は一つの組合せとは限らず、複数存在する。従って、可換を満たすものが\(n\)組ある場合には、\(Nat(\Delta_C,D)=\{(\alpha_1^1,\alpha_2^1),\{(\alpha_1^2,\alpha_2^2),...,\{(\alpha_1^i,\alpha_2^i)\}\)となる。

このようなものを選ぶことができるなら、\(C\)は\(A\)と\(B\)の積の極限への候補となる。

問題1：圏\(\bf{2}\)を利用して、二つの整数の公約数を選び出しなさい。
問題2：圏\(\bf{2}\)を利用して、料理作り好きな友人のリストの候補を作成しなさい。ヒント：知り合いを\(A\)とし、趣味を\(B\)を出発点に考えなさい。ここから絞っていくと、答えの一つとして、\(A\)は料理好きな友達の集まり、\(B\)は仏料理や和食のような種類の集まりを得る。

インデックス圏からの自然変換

圏\(\bf{2}\)をもう少し一般化してインデックス圏を用いてみよう。インデックス圏は、対象にインデックスが付加されており、対象間では射が定義されているものとする。ここでは、インデックス圏の中で最も単純な3つの対象からなるものを利用しよう。下図に示すように、インデックス圏\(\mathcal{I}\)と圏\(\mathcal{C}\)が存在したとしよう。

圏\(\bf{2}\)の場合と同じように、\(\mathcal{C}\)から三つの対象\(D_I,D_J,D_K\)を選んだとしよう。これらには\(\mathcal{C}\)から関手\(D\)で張ることができたとしよう(下図)。

即ち、前回と同じように次が満たされたとする。
\begin{eqnarray}
D_I=D(I) \\
D_J =D(J) \\
D_K=D(K) \\
Df=D(f) \\
Dg=D(g) \\
Dh=D(h) \\
id_{D_I}=D(id_I) \\
id_{D_J}=D(id_J) \\
id_{D_K}=D(id_K)
\end{eqnarray}

次に、\(\mathcal{C}\)から一つの対象\(C\)を選んだとしよう。これらには\(\mathcal{C}\)から関手\(\Delta_C\)で張ることができたとしよう(下図)。

即ち、次が満たされたとする。
\begin{eqnarray}
C=D(I) \\
C =D(J) \\
C =D(K) \\
id_{C }=\Delta_C f =\Delta_C(f) \\
id_{C }=\Delta_C g =\Delta_C(g) \\
id_{C }=\Delta_C h=\Delta_C(h) \\
id_{C }=D(id_I) \\
id_{C }=D(id_J) \\
id_{C }=D(id_K)
\end{eqnarray}

ここで、関手\(\Delta_C\)から関手\(D\)に対して自然変換が成り立ったとしよう(下図)。

自然変換は、ドメインとなった圏の対象ごと、ここではさらに射もあるので射ごとにも、ドメイン側の圏で、移されたものの間を射で結んだ時に、可換を保持しなければならない。これは、圏\(\bf{2}\)の時の説明と同じである。

このため、対象\(I,J,K\)に対して、射\(\alpha_I:C \rightarrow D_I, \alpha_I:C \rightarrow D_J,\alpha_I:C \rightarrow D_K\)が存在し、可換の条件を満たさなければならない。

まず、射\(f\)に対しては、次のことが満たされなければならない(上図)。

即ち、
\begin{eqnarray}
\alpha_J = Df \circ \alpha_I
\end{eqnarray}

同様に射\(g\)に対して、
\begin{eqnarray}
\alpha_K = Dg \circ \alpha_J
\end{eqnarray}
が成り立ち、射\(h\)に対して、
\begin{eqnarray}
\alpha_K = Dh \circ \alpha_I
\end{eqnarray}
が成り立たなければならない。

この結果、下図に示すように、\(C\)を頂点として形作られた三角錐(\(C,D_I,D_J,D_K\))は、そのすべての側面において可換であるならば、自然変換である。即ち、\(\{(\alpha_I,\alpha_J,\alpha_K)\}\)は自然変換\(Nat(\Delta_C,D)\)の一つである。一般にはこのようなものは一つとは限らない。\(i\)個存在するとするならば、自然変換は\(Nat(\Delta_C,D)=\{(\alpha_I^1,\alpha_J^1,\alpha_K^1),(\alpha_I^2,\alpha_J^2,\alpha_K^2),...,(\alpha_I^i,\alpha_J^i,\alpha_K^i)\}\)である。

今回は、3つの対象からなるインデックス圏を用いて三角錐を得た。インデックス圏の対象を増やしていくと三角錐は円錐へと近づいていく。圏論では、インデックス圏から得られるこのような物体を錐(cone)と呼んでいる。

極限の定義はこの錐を用いて定義できるが、その話は次回行う。

極限－例：最大公約数

１．３　最大公約数

前回の記事では、集合を利用して、圏論での積を説明した。また、積の普遍性についても説明した。これらをさらに進めると、極限になる。しかし、もう少し例を挙げて、極限の説明をするための準備をすることにしよう。

ここでは、集合から離れることにする。極限という言葉は使わないが、類似した概念は中学校の数学でも現れる。そう、最大公約数(GCD: greatest common divider)だ。二つの整数が与えられた時に、共通の約数で最大のものが最大公約数だ。

今、二つの整数360と420を選んだとしよう。このとき、二つの整数の共通の素数は、(2,2,3,5)である。従って、これらの中からいくつかを取り出して掛け合わせたものは公約数となる。例えば、(2,2,3)からの12、あるいは、(2,3,5)からの30などはこの二つの数の共通の約数である。また、全てを取り出した(2,2,3,5)からの60は最大公約数である。これらを\(X,X’,A \times B\)とし、360と420を\(A\),\(B\)で表すと、以下のような可換図式を得る。

この図は、前回の記事で積の極限を説明したときの図と同じものである。この図より、\(A \times B\)が、\(A \)と\(B \)の積の極限、すなわち最大公約数、になっていて、\(X\)や\(X’ \)などが、\(A \)と\(B \)の積の候補、すなわち公約数、であることが分かる。従って、候補の中でもっともよいものが極限、すなわち、公約数の中で最も優れたもの、この場合には大きいものが最大公約数となっている。

即ち、上記の図において、\(A\)と\(B\)に対する任意の公約数\(X\)は、最大公約数\(A \times B\)に対して、一意的な射\(m\)が存在し、
\begin{eqnarray}
fst \circ m = p \\
snd \circ m =q
\end{eqnarray}
である。ここで、\(fst:A \times B \rightarrow A \),\(snd:A \times B\)である。これにより、最大公約数は圏での積である。

上記の図は、公約数で表したが、これを、それぞれを構成する素数で表すと次のようになる。

この図で、公約数を、すなわち最大公約数の候補を、それを構成している素数の集合と見なすと、候補は、極限即ち最大公約数の部分集合となっていることが分かる。

これは、前回、集合と説明したときと同じで、その時も候補は極限の部分集合になっていた。このようにみていくと、最大公約数の場合も、前の例題と同じだということが分かる。

このため、個別に定義するのではなく、共通な概念として極限を考えたほうがよいということが分かる。

問題：最大公約数が作る圏をHaskellで作成しなさい。

コテージパイ - ひき肉料理をポテトでトッピングしたイギリス家庭料理

今日、紹介する料理は、イギリスの伝統的な家庭料理、コテージパイ(Cottage Pie)だ。ウィキペディアによれば、この名前が使われるようになったのは1791年で、このころ、ジャガイモが貧困層でも利用できるようになった。

ジャガイモは、ペルー南部のチチカカ湖畔が発祥とされている。ヨーロッパに伝わったのは1570年ごろで、スペイン人が持ち込んだ。その普及は緩やかだったようで、本格的にヨーロッパで栽培されるようになるのは18世紀半ごろ、栽培の推進をしたのはプロイセン王のフリードリッヒ大王である。また、同じころ、アイルランドでは小作農家がジャガイモの栽培を行うようになり、急激にその依存度を高くした。おそらく、この時期に、ジャガイモを利用したコテージパイが食卓に上がるようになったのであろう。

コテージパイはいたって調理が簡単な料理だ。ひき肉を玉ねぎとにんじんと一緒に炒め、その上にマッシュポテトをトッピングして、オーブンで温めるだけだ。料理に使う材料は以下のものだ。

主なものは、牛ひき肉(300g)、ジャガイモ5個、玉ねぎ1個、ニンジン1本だけ、残りは味付け用なので、好みに応じて変えてもよい。

最初に用意するのは、マッシュポテト。ジャガイモの皮をむき、

大きさが均等になるように、1個のジャガイモをそれぞれ12等分する。

今回は、これらをラップして、電子レンジの「茹で根菜」という機能を利用して、調理した。

中まで火が通っていれば、ラップの上に厚い布をかぶせ、指で押せば、マッシュポットができる。今回は、少し硬かったので、中華料理のレンゲの底で押してつぶした。

つぶしている途中で、牛乳大匙2杯、バター10g、塩、黒胡椒をそれぞれ小さじ1/4を混ぜ、マッシュポテトに味付けをする。

玉ねぎ1個とにんじん1本はそれぞれみじん切りにする。

フライパンを温め、オリーブ油をひいて、牛ひき肉を色が変わるまで炒める。

さらに、玉ねぎを混ぜて、これが透明になるまでさらに炒める。

塩小さじ１、黒胡椒を加え、さらにローリエ、ニンジンを加えて、1分ほど炒めた後で、80ccのお湯にマギーブイヨン1個を溶かし、これを加える。
さらに、薄力粉大匙2杯を茶こしを使ってまんべんなくまぶし、トマトペースト(6倍濃縮)を一袋(18g)加えて、水分がなくなるまで、さらに炒める。

にんじん、玉ねぎと一緒に炒めたひき肉を、耐熱皿に移し、平らにする。

その上に、マッシュポテトをのせる。

190度に熱したオーブンで、これを20分間ほど温める。

野菜を付け合わせにして、食卓に出す。今回はインゲンにした。

コテージパイの断面はこのようになっている。

年末の忙しい時期には料理にあまり時間をかけられないので、手間のかからないコテージパイは手ごろな料理である。

今回は、ひき肉に牛を用いたが、イギリスではラムやマトンを用いることもある。この場合には、シェパーズパイ(shepherd's pie)と呼ばれる。トライしてみたいのだが、ラムのひき肉が入手しにくいのが問題だ。

極限－圏論の積

プログラマのための圏論(初級編)では、自然変換まで説明した。ここまで理解すると本当の意味で圏論を自由に扱えるようになる。上級編では、これまでの理解を踏まえて、さらに圏論の奥義を学ぶことにしよう。

１．極限

圏論の特徴は抽象階層だと思う。圏は、対象と射によって構成される構造だ。従って適当に、対象と射を選ぶことによって、圏を作ることができる。下図では、圏\(\mathcal{B}\)は、対象\(A,A’\)と射\(f,f’,f’’\)により構成されている(圏を構成するには、このほかに、合成や恒等射などを必要とするがここでは本質的なものだけで記述する)。

さらに、圏を対象にして、圏と圏との関係を射とすることで、抽象的な圏を作成することができる。この操作を繰り返すことで、より抽象的な圏を得ることができる。

下図では、圏\(\mathcal{B}\)を対象\(B\)にして、新たな圏\(\mathcal{C}\)を構成した。\(B’\)は同じく圏\(\mathcal{B’}\)を対象にしたものである。\(g,g’,g’’\)は圏\(B\)と\(B’\)の間の射である。一般には、\(g,g’,g’’\)は関手と呼ばれ、\(\mathcal{C}\)は小さな圏の圏と呼ばれる。

同じように、圏\(\mathcal{D}\)も構成される。この時、\(h,h’,h’’\)は自然変換と呼ばれる。

逆に、ある圏から、その対象の要素を対象とし、要素間の関係を射とすることで、具体的な圏を作成することができる。この操作を繰り返すことで、より具体的な圏を得ることができる。

対象と射という概念で、抽象階層のどのレベルをも構成できるため、圏の構造はとても規則的で、簡潔であると言える。

圏論では、あらゆる種類の中で成り立っているような普遍的な性質を表現することを一つの目標とする。圏論の教科書を開くと様々な普遍性を見つけることができる。その中で、抽象階層の有用性を教えてくれる普遍性は極限だと思う。中学校では、最大公倍数や最小公倍数などを習ったし、高校では関数の最大値・最小値や無限数列の極限値などを学んだ。これらは、ある性質を有するものの並びの中で、極限にあるものを求めている。

それでは、圏論での極限がどのようなものであるかを見ていこう。極限の説明は、圏での積を用いて行われていることが多いので、ここでも、積を用いて説明しよう。

１．１　圏での積

圏論は、対象を定義しなければならない、ここでは、まず、\(A\)と\(B\)を対象としよう。そして、この積を\(A \times B\)で表すことにしよう。次に、射を定義することにしよう。ここでは、\(A \times B\)から\(A\)への射\(fst\)と\(A \times B\)から\(B\)への射\(snd\)とで表すことにしよう。図で表すと次のようになる。

\(A\)と\(B\)が集合の場合には、積はデカルト積と呼ばれ、それぞれの要素\(a \in A\)と\(b \in B\)の対(a,b)で表すことができる。対として表した時、最初の要素が\(A\)に、二番目のそれが\(B\)に属すという意味で、分かりやすくするために便宜的に、射\(fst\)と\(snd\)を用いた。このため、\(fst\)と\(snd\)である必然性はないので、一般的によく用いられている\(\pi_1\)と\(\pi_2\)であってもよい。

圏で用いられている対象、射、積を漫然と理解したままで次に進むと罠にはまってしまうことが多いので、ここでは、これらの概念を具体的な例を用いて、より詳しく理解することにしよう。

圏での積は、乗算であったり、論理積であったりするが、ここでは、論理積と考えることにしよう。また、対象は、連続的な空間であったり、有限の要素の集合であったりするが、ここでは、まず、有限な要素の集合とする。そして、次のような問題を考えることにしよう。

例題1

「ある学年での\(A\)組のクラスで体育会系の部に属していた男女のペアそれぞれについて、同じ部に属していたかどうかを弁別する」プログラムを考え、先の対象\(A \times B\)を何にしたらよいかを考えることにしよう。

このプログラムは、条件「\(A\)組のクラスで体育会系の部に属していた男女のペア(これは、単一でも複数であってもよいとする)」を満たすもののみ受け付けることでき、そうでない場合には、受け付けず処理を行わないものとする。プログラムが受け付けた場合、同一の体育会系の部に属している場合には\(True\)を、異なる体育会系の部に属している場合には\(False\)を返すものとする。そして、プログラムが受け付けてくれるものを\(A \times B\)の候補ということにしよう。

例えば、\(A\)組テニス部所属\(B1\)君と\(A\)組水泳部所属\(G1\)さんの\(P1=(B1,G1)\)をプログラムに入力したとしよう。二人とも\(A\)組に属し、体育会系の部に属するので、プログラムは受け付けてくれ、\(False\)が返ってくる。従って、\(p1\)は\(A \times B\)の候補である。

次の例はどうであろうか。\(B\)組所属の男子\(b2\)と\(A\)組テニス部所属の女子\(G2\)の対\(P2=(B2,G2)\)をプログラムに入力したとしよう。男子が\(A\)組でないので、このプログラムはこの入力を受け付けない。このため、\(P2\)は候補とならない。

それでは、\(A\)組卓球部所属の男子\(B3\)と\(A\)組ダンス部所属の女子\(G3\)の対\(P3=(B3,G3)\)をプログラムに入力したとしよう。この入力は受け付けられる。このため、\(P3\)は候補となる。

このようなことを繰り返し行ったとすると、いくつもの候補が上がるであろう。その中で、不足することなく条件に合う対となっているのはどれであろうか。\(A\)組体育会系の部に所属する男子\(Bas\)と\(A\)組体育会系の部に所属する女子\(Gas\)の対であることは容易に分かる。

これを図で表してみよう。\(P1\)と\(P3\)と\(Bas \times Gas\)が候補であり、\(A \times B = Bas \times Gas\)が条件を満たす最大の集合であることが分かったので、次の可換図式を得る。図において\(incl\)は包含関数である。

この例で、\(A \times B \)の候補となるのは、\(Bas \times Gas\)の部分集合であることが分かる。

例題2

先の例は離散系であったので、今度は連続した空間での例を挙げることにしよう。ある地域\(R\)の標高と年間平均気温の関係を表すことを考えよう。今、標高の方は赤色で表すことにし、高いほど濃くなるようにした。また、気温の方は黄色で表すことにし、低いほど濃くなるようにした。これらの色は絵の具で混ぜることにした。従って、標高が高く気温が低いほど、橙色は濃くなり、反対の場合には薄くなる。

標高を赤色で表した地域\(R\)の地図を\(A\)とし、年間平均気温を黄色で表した\(R\)の地図を\(B\)とした時、このような地図をその一部でも作成できるようなものを探すこととしよう。前の例に習って、これを\(A \times B\)の候補と呼ぶことにしよう。

\(R\)内のある地点\(R1\)での標高を\(P1_h\)とし、その地点での年間平均気温を\( R1_t\)とした時、\(R1=(R1_h, R1_t\)は、求められている地図の一部を描くことができるので、候補となる。

\(R\)の隣の地域\(R2\)での標高を\(R2_h\)とし、そこの年間平均気温を\( R2_t \)とした時、\(R2=(R2_h, R2_t)\)は、求められている地図の範囲外であるので、候補とはならない。

\(R\)に含まれる小さな地域\(R3\)での標高を\(R3_h\)とし、そこの年間平均気温を\( R3_t \)とした時、\(R3=(R3_h, R3_t)\)は、求められている地図の一部を描くことができるので、候補となる。

\(R\)に含まれる小さな地域\(R4\)での標高を\(R4_h\)とし、\(R\)内の別の地域\(R4’\)の年間平均気温を\( R4’_t \)とした時、\(R4=(R4_h, R4’_t)\)は、求められている地図の一部を描くことができないので、候補とならない。

\(R\)に含まれる小さな地域\(R5\)での標高を\(R5_h\)とし、\(R5\)の年間日照時間を\( R5_s \)とした時、\(R5=(R5_h, R5_s\)は、求められている地図の一部を描くことができないので、候補とならない。

これらの関係を可換図式で示したのが、下図である。

この例でも、\(A \times B \)の候補となるのは、\(R_h \times R_t\)の部分集合であることが分かる。

１．２　積の定義

圏では積は次のように定義される。

\(\mathcal{C}\)を適当な対象\(A,B\)を有する圏とする。\(A\)と\(B\)の積は、\(A \times B\)と書かれる\(\mathcal{C}\)の対象と二つの射\(fst : A \times B \rightarrow A \)および\(snd : A \times B \rightarrow B \)との組で、以下の普遍性を満たすものをいう。

積の普遍性

任意の対象\(X\)(これは例題1，2では候補と呼んでいたもの)および射の対\(p:X \rightarrow A\)および\(q:X \rightarrow B\)が与えられた時、一意的な射\(m : X \rightarrow A \times B\)が存在して、下図

を可換にする。

上の定義から、この圏では、\(A\)と\(B\)への射を有するどのような対象を持ってきたとしても、積の普遍性が満たされる。即ち、\(A\)と\(B\)への射\(p'\)と\(q'\)を有する任意の対象\(X’\)を持ってきたとしても下図のように可換性が成り立ち、一意的な射\(m’ : X’ \rightarrow A \times B\)が存在する。

このことから、このような全ての対象(例題1，2で候補と言っていたもの)の中で、\(A \times B\)が\(A\)および\(B\)への最も優れた射(射の合成として表されないという意味で優れたということにする)を与えることから、極限ともいわれる(ただし、極限はのちの説明ではもっと一般的に使う。候補の中で、どれよりも優れた射を有するものと理解して欲しい)。

理解を深めるためには、次の問題を解くことを勧める。

問題1：例題1をHaskellで実現しなさい。
問題2：例題2をHaskellで実現しなさい。

縄文時代のモラルと家族システム

神奈川歴史研究会の9月の例会で発表した報告書を転載します。

縄文時代のモラルがどのように形成され、どのような家族システムを構築したかについて論じています。

弥生時代の土偶形容器を横浜市歴史博物館に見学に行く

文明の衝突は社会を激震する。律令制や明治維新はその代表的なものだが、弥生時代の到来もそれに劣らない文明の衝突であった。

弥生時代に先立つのは縄文時代である。この時代は、1万年もの長きにわたって続き、人々は狩猟採集の定住生活を享受していた。この当時の人びとは、食糧確保のために費やす時間はそれほど多くはなかったと推察されている。傍証になるが、定住はしなかったが、同じように狩猟採集生活を送っていたオーストラリア先住民のアボリジニの人々は、食糧獲得のために、4時間半程度しか使っていなかった。彼らは、余剰の時間を音楽や絵画に振り向けていたが、縄文時代の人々はどのように振り分けていたのであろうか。

その一端を伺わせてくれるのが、時間をかけて丁寧に作成されたと見られる、土器や土偶である。縄文時代の中期になると、燃え上がる炎をかたどったような装飾性溢れる火焔型土器が出現する。同じころ、長野県の八ヶ岳山麓の遺跡では「縄文のビーナス」と呼ばれる土偶が、後期の初めになるとそこから4㎞離れた地点で「仮面の女神」と称せられる土偶が造られた。また、東北地方でも後期には、合掌土偶や遮光土偶が造られている。

男女間での分業が行われていた縄文時代には、土器や土偶は女性により製作された。得意のおしゃべりをしながら余剰の時間をこれらの製作を通して楽しんだのであろう。他方の男性は余剰の時間をどのようにつぶしたのであろう。これは推察の域を出ないが、食料確保を兼ねながらスポーツとして狩猟を楽しんだのだろうか。

しかし、楽しんでばかりもいられなかった。縄文時代も晩期になると、これまで温暖であった気候は寒冷化し、現在よりも気温で2度程度低下し、縄文集落が集中した信州の山々には深い雪が降り、関東の海岸線は後退して、狩猟採取生活が困難になる。縄文時代最盛の中期には26万人程度の人々が住んでいたが、晩期には8万人程度に落ち込んだ。

縄文の人々が困難を極めている頃、新しい文明がもたらされた。朝鮮半島からの水田稲作技術を携えた人々の渡来である。今から3000年前のことで、九州北部で始まった。

水田稲作で特徴づけられる弥生時代の文化は、狩猟採集による縄文時代のそれとは大きく異なっていた。縄文時代の社会が家族あるいは拡大家族を中心とした共同体であったのに対し、弥生時代は血縁関係を超えた大きな集団が形成され、それを統率するようなリーダーが出現し、社会が階層化し始めるような社会であった。水田稲作は、水田の管理・運営に多大の労力を必要とするだけでなく、従事者間での協力や秩序を必要とする。水田稲作によって、多くの人々は土地に縛られ、離れられない状態になる。他方で、人や水田を管理するような人も現れる。

仲間内で諍いが起きたとき、縄文時代は他の場所に居住地を求めて去れることが容易に行えたが、弥生時代は水田に縛られているため、他の場所に移動することは容易ではなかった。このため、諍いが起こらないようにすることで生じるストレス、そして、諍いが生じたときにそれを解決しようとすることに起因するストレスは、それ以前とは比較にならないほど大きかった。他の言葉を借りるなら、縄文時代とは異質のモラルを弥生時代は必要とした。

さらには、収穫物である米や生産するための水田を狙っての集落の間での収奪も生じる。このため、部族間での対立を解決するための対策や方策も必要とした。

縄文時代は血のつながりを認識できるような人々の集まり、部族社会であったのに対し、弥生時代には、集団を統率する人が現れ、社会が階層化しはじめた。即ち、古墳時代に本格化する首長社会への移行期である。古墳時代になると地方豪族が大きな集団をまとめるようになり、さらに、ヤマト政権が誕生して原始国家が成立するようになる。

残念なことに、水田稲作をいったん始めてしまうと、かつての狩猟採集生活に戻ることはできない。単位面積当たりで獲得できるカロリー量では、水田稲作は圧倒的に勝る。このため、水田稲作を始めてしまうと人口が急増し、狩猟採集では維持できないほど多くの人々が居住してしまい、縄文時代の生活に戻ることは不可能になる。

水田稲作という新しい文明が日本列島に入り込んできたとき何が起きたであろうか。縄文時代の生活を維持していた在地の人々は、水田稲作を携えてやってきた渡来の人びとを、すんなりと受け入れたのであろうか。あるいは、撃退しようとしたのであろうか。逆に、撃退されたのであろうか。

関東地方に水田稲作がもたらされたのは、だいぶたってからのことである。横浜では大塚遺跡が有名であるが、ここに伝わったのは弥生時代中期後葉、2000年前ごろとされている。九州北部にもたらされてから1000年もたってからのことである。水田稲作を生業とする集落は、他集落からの攻撃に備えて、環濠で守られている。環濠は、集落の周りをV字型や逆台形の深い溝(大塚遺跡の場合は幅4.5m深さ2.5m)で囲んだ構造物である。大塚集落は、環濠集落全体が発見された、貴重な遺跡である。

小田原市の中里遺跡は、関東地方では最初期の弥生集落である。大塚遺跡から発見された土器は宮ノ台式土器であるが、この遺跡からはその一つ前の世代の中里式 (須和田式) 土器が出土している。中期中葉と呼ばれる時代に属す。

中里遺跡の北5㎞のところには、弥生時代前期前葉、およそ2500年前、の中屋敷遺跡がある。この遺跡からは炭化米が発見されている。関東地方での水田稲作の到来については解明されていない点が多いものの、この遺跡はこれを研究する上で貴重な存在と考えられている。

中屋敷遺跡は昭和女子大学が発掘調査を行っている。調査に当たっている人たちが女性だけというユニークさも手伝って、興味のある場所である。

ここから発掘された小型の精製品の土器は、縄文時代晩期以降の形式を踏襲しており、縄文文化が根強く残っていることを伺わせる。そして、面白いのは、土偶形容器だ。

先週まで、横浜市歴史博物館で、「横浜に稲作がやってきた」という特別展示が開催され、この土偶が展示されていた。そこで、文明の衝突の一端でも知ることができればと思い、見学に行った。
正面から見ると、

顔の表情が豊かで、入れ墨も施されている。普通の女性なのだろうか、それとも、祭祀と関係のある特別な人なのだろうか。縄文時代の土偶はほとんどが女性だ。この土偶も胸の表現があるので女性だろう。土偶と言えば、縄文時代を代表する遺物で、弥生時代には存在しないと思われているが、そのようなことはな。非常に少なくなるが400体ほど発見されている。その中で、土偶形容器と呼ばれるものもおよそ40体ほど見つかっている。土偶形容器は男女一対で作られることが多いので、対の男性の方はまだ地下で眠っているのだろうか。

上の方から見ると中空の容器のようになっていることが分かる。

容器の中には、骨が入っていたそうで、新生児の骨と鑑定されている。土偶が墓の副葬品として利用されることは縄文時代にはほとんどなかったが、晩期後半には東海地方ではそのように用いた例もあるそうだ。また、この容器の中に新生児といえどもそのまま入れることはできなかったと思われるので、一度埋めた後、その骨を取り出して容器の中に収めたと思われる。縄文時代後・晩期には再葬が広く行われるようになっていたが、その傾向をひくものだろう。また、弥生時代初期には、蔵骨器を用いた壺型再葬墓が発達するがその流れにも沿ったものである。

中屋敷遺跡の状況を見る限り、縄文時代からの継続性を読み取ることができる。また、炭化米の出現が示唆するように弥生文化の到来が近くまで迫っているが、新しい文化からそれほど大きな影響を受けているようには思えない。しかし、水田稲作文化の影響を本格的に受けるのは、この後であろうから、その時、どうであったかについては判断を下すことはできない。

中屋敷遺跡から発見された大型の土器も展示されていた。

これらには弥生時代の条痕文の模様がついている。写真の下の方に小型の土器が写っているが、残念ながら、これらの土器の原形の部分が破片に近かったので写真を撮るには至らなかった(この記事を書いている段階では、縄文時代の模様が記録として残らず残念なことをしたと感じている)。

特別展示を見た後、大塚遺跡も見て回ったので、その時の写真も載せておこう。
環濠はこのようになっている。

竪穴住居跡は、

復元された竪穴住居は、

掘立柱建物跡には高床倉庫が復元されている。

大塚遺跡の規模は2.2ha、竪穴住居の数は85軒、使用された年数は50年程度、各住居跡で3～5回程度建て替えられたと考えると同じ時期に立っていた住居はおよそ20軒、各住居に5人程度住んでいたとすると、同時期の居住者の数はおよそ100人と考えられている。遺跡は、1/3ほど残されていて、夜間を除いて見学できるようになっている。

また、隣接して、歳勝土遺跡がある。ここは、大塚遺跡の人たちの墓地と考えられていて、弥生時代の代表的な墓制の一つである方形周溝墓が30基ほど発見されている。
木棺が埋められた状況が復元されている。

また、墓の全体もわかるようになっている。

関東地方では、立派な土偶を見ることは少ないが、今回は、弥生時代のものとは言え、優れた土偶を見学することができ、とてもよかった。特別展示の入口には土偶形容器が、出口には人面付土器(横浜市上台遺跡)が置かれていた。これは、弥生時代後期のものであった。中期までは再葬墓として用いられていたが、これは集落から発見されたそうで、その用途が変化したのだろう。およそ1000年の弥生時代の変化を知ることもでき、良い展示であった。

都内世田谷区の荏原台古墳群を訪れる

11月3日は晴れの日が多い特異日である。この日は雨が降ると天気予報ではずっと伝えられていたが、前の日になって、急に晴天になると変更された。そのとおり、雲一つない素晴らしい日になったので、前の日の埼玉古墳群に続いて、荏原台古墳群を訪れた。

訪問の一つの理由は、思い出の地だからである。荏原台古墳群は田園調布と野毛の二つの地域に分かれている。田園調布では、駅の近くにある教会で結婚式を挙げたし、短い期間だが生活したこともある。野毛は高校3年生の夏にテニスに明け暮れたところだ。

埼玉古墳群と荏原台古墳群の間には、因縁があるというのももう一つの理由だ。後で詳しく説明するが、荏原台古墳群の豪族が先に台頭し、その後で、埼玉古墳群(あるいはその近く)の豪族が台頭してきて、両豪族の間で、「武蔵国造の乱」が起きたのではないかと見なされている。

それでは、野毛の地域を紹介しよう。ここは、大井町線の等々力駅が最寄り駅だ。景色を楽しむために、等々力渓谷を経由する。夏でもひんやりとしていて、渓谷という名に恥じないところだ。渓谷の様子をいくつか示そう。多くの人が散歩を楽しんでいる。


高校3年生の時にテニスで利用したところは、企業の保養所で半分は建物と庭園、半分はテニスコート3面になっていた。テニスコートは住宅に変わっていたものの、残りの部分は日本庭園として活用されていた。

ここからそれほど遠くないところに、野毛大塚古墳がある。ここは、帆立貝形古墳がある。全長82mで5世紀前半の築造だ。埼玉古墳群に先んじていることが分かる。

この古墳の模型もあった。

等々力駅に戻って、東横線の多摩川駅で下車して、荏原台古墳群のうちの田園調布の地域を訪ねる。多摩川の堤の上にあり、眺めがよい。人気高い住宅街となっている武蔵小杉を望むことができる。

この台地にはかつて調布浄水所があったそうで、跡地は次のようになっている。

しばらく歩くと、亀甲山古墳の案内がある。この地域最大の古墳で4世紀後半から5世紀前半の築造で、全長は107mである。樹木に覆われているため、全容を見ることはできない。

さらに歩くと、多摩川台古墳群1～8号墓の案内がある。

それぞれの墓には、場所を示すだけの板が置かれているだけだ。付近を見ても墓らしい様子を知ることはできない。

しかし、墓とは反対側の田園調布の景色はきれいだ。結婚式を挙げたカトリック田園調布教会も見ることができた。

さらに歩くと、前方後円墳の宝莱山古墳を右手にし、左の方に曲がると宝莱公園になる。公園を出ると、駅へと繋がる銀杏並木がある。

さらに進むと、懐かしい駅舎が現れる。

しかし、この駅舎は駅の業務をしていない。面影だけを残しているモニュメントだ。かつては駅舎の向こう側にはホームがあった。しかし、今は、モニュメントの駅舎を抜けると、本当の駅舎へ向かうための階段が現れる。昔の田園調布の駅前の雰囲気がとても良かったので、その雰囲気を残すために、そのままの姿で残されたのであろう。

歩いたコースの説明が終わったので、荏原台古墳群と埼玉古墳群の関りを説明しよう。

この当時の世界情勢から始めよう。『日本書紀』の継体21年(527)・22年(528)の条には、『筑紫国造磐井』の「叛逆」事件の伝承がある。

この伝承に対して、戦前からこれまで様々な解釈が試みられてきた。今日では、東アジアの国際情勢とのかかわりあいを重視して、「磐井は、この頃、九州の筑紫・火(肥)・豊の諸国に勢力を張り、朝鮮半島の高句麗・百済・新羅諸国と積極的に外交を行い、一つの王国を形成しつつあったことがうかがえる」と見られている(佐藤信)。

当時の日本列島は、「王(キミ)」と呼ばれる地方豪族が存在し、王たちが連合的関係を作り、その中心の王を「大王(オオキミ)」と呼んでいた。大王はのちに天皇になるが、この当時の大王と王の関係は上下関係ではなく、同盟関係に過ぎなかった。

磐井も筑紫君磐井と呼ばれた。君と王とは「キミ」は同音であり、磐井は「王」であった。

磐井の乱と同じように地方豪族との戦いが、同時期に関東にもあったことが伝承されている。これは「武蔵国造の乱」である。『日本書紀』安閑元年(531)閏12月条に記載されているが、そこに、「王」と同音の「君」を用いた、上毛野君小熊が出てくる。大王に対抗できるような王が関東にいたのであろう。『日本書紀』には次のように書かれている。

武蔵国造笠原直使主(オミ)と同族小杵（オギ）と、国造を相争ひて、[使主・小杵、皆名なり。]　年経るに決め難し、小杵、性阻くして逆ふこと有り。心高びて順ふこと無し。密に就きて援を上毛野君小熊に求む。而して使主を殺さむと謀る。使主覚りて逃げ出づ。京に詣でて状を言す。朝廷臨断めたまひて、使主を以て国造とす。小杵を誅す。国造使主、悚憙懐に満ちて、黙已あること能はず。謹みて国家の為に、横渟、橘花、多氷、倉樔、四処の屯倉を置き奉る。

この伝承は、笠原直使主と同族の小杵が武蔵国造の地位を争ったとき、その加勢を、使主は朝廷(大王)に求め、小杵は上毛野君(王)に求めたというものだ。磐井と同じように、上毛野は大君と争うほどの勢力があったことが分かる。また、横渟は横見郡(埼玉県)と、橘花は橘樹郡(川崎市)、多氷は多摩郡(東京都)、倉樔は久良岐郡(横浜市)と比定されている。

滅びてしまった小杵だが、彼はどこに住んでいたのであろうか。二つの説があり、一つは南武蔵(亀甲山古墳や芝丸山古墳など)、他の一つは(比企地方の古墳群)である。なお、使主は埼玉古墳群と比定されている。

埼玉古墳群稲荷山古墳からは鉄剣が出土している。辛亥年と銘があり、471年と531年の説があるが、前者の方が有力である。また、銘文の解釈は一つではないが、中央豪族のワカタケル大王(倭王武)からこの地域の豪族ヲタケに下賜されたというのが有力である(大王が中央豪族ではなく関東の豪族という説がある)。もし、これが正しければ、同盟関係から従属関係へと移行していたことをうかがわせる。

鉄剣を下賜されたヲタケと笠原直使主の関係も明らかではないが、何らかの関係があるとすれば、笠原直使主が朝廷を頼ったこともわかりやすい。

さて、小杵が南武蔵の豪族であったとすると、彼らが残した古墳は荏原古墳群であったと思われる。この古墳群は、先に述べたように、田園調布の地域と野毛の地域に分かれる。

まず、田園調布の地域に、4世紀前半には全長97mの宝莱山古墳が、後半から5世紀前半には全長107mの亀甲山古墳が出現する。これらの古墳は前方後円墳である。この後、この地域には6世紀前半まで、古墳は出現しない。

5世紀になると、古墳の位置は野毛の地域に移動し、全長86mの野毛大塚古墳、全長30mの八幡塚古墳、全長57mの御嶽山古墳が出現し、八幡塚古墳は円墳であるが、残り二つは帆立貝形古墳である。

6世紀になると、再び田園調布に戻るが、古墳は小型である。6世紀前半に小型前方後円墳の浅間神社古墳、6世紀後半から7世紀中ごろにかけて多摩川台古墳8基(二つは小型前方後円墳、残りは円墳)、6世紀末に前方後円墳と思われる観音塚古墳が出現し、7世紀中・後期には古墳は築造されなくなり、横穴墓となる。

小杵が敗れたのは6世紀の前半であるので、この当時田園調布に築造された古墳が小型になる。この点をとらえて、甘粕健は「武蔵における古墳時代の有力古墳の分布が、前期の武蔵南部から後期には武蔵北部(埼玉古墳群)に移動したことも、「武蔵国造の乱」とかかわりがあると指摘している。

このように遠く離れた二つの地域が、歴史の中でつながりがあったことを知るのは楽しいことである。

全国有数規模の埼玉古墳群を訪れる

弥生時代の遺跡を2か所ほど立て続けに訪問したので、それに続く、古墳時代の遺跡を訪ねることにした。

この時代の象徴的な墓は前方後円墳である。前方後円墳と言えば、近畿地方と思いがちだがそうではない。全国に広がっていて、関東地方にもたくさん存在する(前方後円墳が一番多い県はなんと千葉県で約720基存在する)。埼玉県行田市の埼玉(さきたま)古墳群は、全国有数の規模を誇り、10基余りの前方後円墳が集中している。近畿地方には、全長が200mを超えるものが存在する(最大のものは大仙陵古墳で486m)ので、それらには匹敵しないが、ここには100mを超えるものが3基存在する。

10月2日も天気に恵まれたので、電車が空きはじめたころに家を出た。横浜方面から埼玉県へ向けての移動は、新宿湘南ラインができてから、とても便利になった。この日も、渋谷駅まで出た後、そこからは最寄り駅まで一本で行けた。但し、最寄り駅と言っても、古墳群まではかなりある。行田駅から「観光拠点循環コース」を利用すれば古墳群まで運んでくれるのだが、一日7便しか出ていない。どれも都合のよい便ではなかったので、一つ前の吹上駅で降りて路線バスを利用した。

吹上駅からの路線バスでは、佐野経由を利用するとよい(行先表示変化中にシャッターを押したため、表示が明瞭でない)。

残念ながら、路線バスは古墳群には行かない。このため、最も近い停留所「産業道路」で降り、そこから15-20分歩かないといけない。産業道路の一つ前の停留所は「佐野団地」。ここまでは、バスは駅からまっすぐに進んでくる。そして、産業道路の停留所の手前で左折する。バスを降りた後、去って行くバスとは反対方向にひたすらまっすぐ歩いていくと、埼玉古墳群に至る。ここは大きな公園になっている。

全ての古墳を見学するコースは1時間半ほどかかると説明にあった。遠路をはるばるやって来たので、全てを見学することにした。見学した順番ではなく、古墳ができた順に従って説明しよう。

前方後円墳は近畿地方では3世紀ごろに始まり6世紀になると規模が小さくなるが、埼玉古墳群はこれとは反対に6世紀に盛んになる。

埼玉古墳群の中で最古の古墳は、稲荷山古墳である。時期は5世紀後半である。全長120mの前方後円墳だ。

古墳の頂まで登れるようになっているので、上を目指す。

この古墳からは、後で紹介するが、文字が刻まれそこに金が埋められた鉄剣が出土している。下の写真のように埋葬されていたそうだ。

二子山古墳は6世紀前半に築造された。全長138mの前方後円墳で、埼玉古墳群の中では最も大きい。古墳の一部が損傷しているということで、修復工事が行われていた。

丸墓山古墳も6世紀前半に築造された。ここの古墳群の中では唯一の円墳で直径105m、日本最大規模の円墳である。1590年の小田原征伐の時に石田三成が忍城攻略のために陣を張った場所としても有名である。また、古墳に沿って半円形に石田堤が掘られている。写真の中で、手前に茶色に帯びたすすきがあるが、そのあたりである。

瓦塚古墳も6世紀前半の前方後円墳である。資料館のそばにあり、全長は73mである。

奥の山古墳は6世紀中ごろ、全長70mの前方後円墳である。

愛宕山古墳は6世紀中ごろに築造され、全長63mで最も小さい前方後円墳である。

鉄砲山古墳は6世紀後半の前方後円墳で、全長は109mである。二子山、稲荷山古墳に次いで大きい。

将軍山古墳は6世紀末、全長90mの前方後円墳である。古墳には埴輪が配置され、往時の姿を彷彿とさせている。

また、「将軍山古墳展示館」があり、古墳の内部に入れるようになっている。石室の側壁には房州石が使われ、千葉県の富津市あたりから運ばれてきたものとみなされている。

内部には埴輪も展示されている。

さらに埋葬の様子も分かるようになっている。

中の山古墳も6世紀末の前方玖円墳で、全長は79mである。

最後に紹介するのがさきたま遺跡の資料館だ。ここには、国宝がいくつも紹介されている。その中でも、一番貴重なのは稲荷山古墳から出土した、金錯銘鉄剣だ。

鉄剣の表と裏には金の文字で、鉄剣の由来が書いてある。それによれば、辛亥の年(471年)に、この刀はワカタケル大王(雄略天皇)からヲタケに贈られた。ヲタケの祖先は代々、杖刀人首(じょうとうじんしゅ、親衛隊長)を務めていた。そして、ヲタケはワカタケル大王に仕え、天下を治める補佐をしていたと記されている。これより、ヤマト王権の力が、東国関東にまで及び、この地方の豪族と同盟関係あるいは主従関係にあったことが分かる貴重な資料である。

展示室は、蛍光灯の光が邪魔をして、撮影するには不向きな環境であったが、国宝の大刀、鉄剣、鉄鏃、帯金具、辻金具、鉸具(かこ)、画文帯環状乳神獣鏡、銀環、勾玉などの国宝が整然と展示されていた。

また、埴輪も展示されていた。

小春日和に恵まれたこの日、広場では、幼稚園児や小学生たちが、遠足なのだろう、広々とした芝生の上を楽しそうに走り回っていた。弥生時代の子供たちもこのように戯れていたのだろうかと思いを巡らしながら、電車が混まないうちに少し早めに帰宅への途に就いた。