Haskellで学ぶ圏論・ウォームアップ編 グラフ

１．グラフ

グラフはいろいろな場面で使われる便利な表記法である。グラフはノードとエッジを有する。図で表す時は、ノードは点でエッジは点と点とを結ぶ矢印として記述される。グラフの例を一つ上げると下図のようになる。

２．圏論

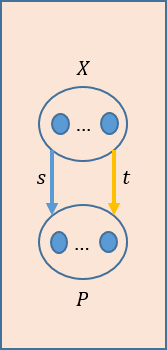
グラフは圏論では、次のように表される。ノードの集まりは集合\(X\)とみなされ、対象となる。エッジの集まりも集合\(P\)とみなされ、対象となる。エッジには始点(のノード)と終点(のノード)があるが、エッジから始点と終点のノードへの写像は射となる。ここでは、それぞれを\(s\),\(t\)とする。先ほどのグラフは圏論では以下の図のように表される。

上記の圏の構成を示すと以下のようになる。
(1)対象：集合\(X=\{a,b,c,d,e\}\)と集合\(P=\{u,v,w,x,y,z\}\)
(2)射：\(s\)と\(t\)
(3)ドメインとコドメイン：\(s,t: X \rightarrow P\)
(4)恒等射：\(id_X : X \rightarrow X\)と\(id_P : P \rightarrow P\)
(5)合成：\(s\)と\(t\)の間での合成写像

上記のグラフを一般化すると、グラフの圏は下図のように表すことができる。

３．グラフ間の写像

写像付きの集合と同じように、その構造を保ちながら、グラフの間で写像を定義することが可能である。グラフ間の写像は、以下の図のようになる。

ここで、\(f\)は二つの写像で構成されている。一つはエッジの集合間での写像\(f_A:X \rightarrow X' \)であり、もう一つはノードの集合間での写像\(f_N: P \rightarrow P\)である。
\(f\)が構造を保った写像となるためには、次の条件を満たす必要がある。
\begin{eqnarray*}
f_N \circ s & = & s' \circ f_A \\
f_N \circ t & = & t' \circ f_A
\end{eqnarray*}

４．始対象と終対象

ここでも、グラフの始対象と終対象について考えることとする。始対象は、写像付きの集合の場合と同様で、空集合である。
終対象に対しては、エッジとノードの集合の要素がそれぞれ一つ、即ち、\(a'\)と\(x'\)であるグラフを考える。一般的なグラフから、このグラフへの写像は次のようになる。

上記の図で、任意の\(a \in X\)に対して

\begin{eqnarray*}
(f_N \circ s) (a) & = & x' \\
(s' \circ f_A) (a) & = & x' \\
(f_N \circ t) (a) & = & x' \\
(t' \circ f_A) (a) & = & x'
\end{eqnarray*}
が満足されるので、構造が保たれていることが分かる。さらに、\(a'\)が一つの点であることから\(X\)から\(X'\)への写像は一つしか存在しない。同様に、\(x'\)も一点であることから、\(X\)から\(X'\)への写像も一つしか存在しない。この結果、写像\(f\)は一つしか存在しないことになり、終対象の条件を満たすことになる。従って、グラフでは、エッジとノードの集合の要素がそれぞれ一つであるグラフが終対象となる。

上記の例だと、エッジとノードの集合の要素がそれぞれ一つであるグラフは、ノードが\(z \)でエッジが\(c \)のグラフである（\(s,t:X' \rightarrow P' \)）。図で表すと以下のようになる。

この終対象を明示すると上記のグラフの圏は次のようになる。
(1)対象：集合\(X=\{a,b,c,d,e\}\)、集合\(P=\{u,v,w,x,y,z\}\)、集合\(X'=\{c\}\)、集合\(P'=\{z\}\)
(2)射：\(s\), \(t\), \(f_A\), \(f_N\)
(3)ドメインとコドメイン：\(s,t: X \rightarrow P\), \(s|X',t|X': X' \rightarrow P'\), \(f_A: X \rightarrow X'\), \(f_N: P \rightarrow P'\)
(4)恒等射：\(id_X : X \rightarrow X\), \(id_P : P \rightarrow P\), \(id_{X'} : X' \rightarrow X'\), \(id_{P'} : P' \rightarrow P'\)
(5)合成：\(s\),\(t\),\(f_A\),\(f_N\)の間での合成写像

この圏をHaskellで記述すると次のようになる(なお、終対象では\(Z \)と\(C \)はそれぞれ\(Z' \)と\(C' \)で示した。

module Graph where

data SetX = A | B | C | D | E deriving (Show, Eq)
data SetP = U | V | W | X | Y | Z deriving (Show, Eq)

data SetXOne = C' deriving (Show, Eq)
data SetPOne = Z' deriving (Show, Eq)

mapS :: SetX -> SetP
mapS x
  | x == A = X
  | x == B = Y
  | x == C = Z
  | x == D = X
  | x == E = U
  | otherwise = error "Unidefined source."

mapT :: SetX -> SetP
mapT x
  | x == A = Y
  | x == B = Z
  | x == C = Z
  | x == D = W
  | x == E = V
  | otherwise = error "Unidefined source."

mapSOne :: SetXOne -> SetPOne
mapSOne x
  | x == C' = Z'
  | otherwise = error "Unidefined source."

mapTOne :: SetXOne -> SetPOne
mapTOne x
  | x == C' = Z'
  | otherwise = error "Unidefined source."


idX :: SetX -> SetX
idX x
  | x == A = A
  | x == B = B
  | x == C = C
  | x == D = D
  | x == E = E
  | otherwise = error "Unidefined source."

idP :: SetP -> SetP
idP x
  | x == U = U
  | x == V = V
  | x == W = W
  | x == X = X
  | x == Y = Y
  | x == Z = Z
  | otherwise = error "Unidefined source."

idXOne :: SetXOne -> SetXOne
idXOne x
  | x == C' = C'
  | otherwise = error "Unidefined source."

idPOne :: SetPOne -> SetPOne
idPOne x
  | x == Z' = Z'
  | otherwise = error "Unidefined source."

funcA :: SetX -> SetXOne
funcA  x
  | x == A = C'
  | x == B = C'
  | x == C = C'
  | x == D = C'
  | x == E = C'
  | otherwise = error "Unidefined source."

funcN :: SetP -> SetPOne
funcN  x
  | x == U = Z'
  | x == V = Z'
  | x == W = Z'
  | x == X = Z'
  | x == Y = Z'
  | x == Z = Z'
  | otherwise = error "Unidefined source."

これを実行すると次のようになる。

*Graph> (funcN . mapS) A
Z'
*Graph> (mapSOne . funcA) A
Z'
*Graph> (funcN . mapT) B
Z'
*Graph> (mapTOne . funcA) B
Z'

５．写像連鎖の果ての終対象

前の記事で、終対象を集合間の写像を連鎖させて得る方法を学んだ。写像の連鎖では、写像が全射であることと、写像される集合のほうが写像する集合よりサイズが小さいことが条件であった。これを繰り返すことで、終対象に至るが、グラフの場合には、ノードやエッジをその構造を保ちながら減らす。保持する条件は、最初の方で述べたが、
\begin{eqnarray*}
f_N \circ s & = & s' \circ f_A \\
f_N \circ t & = & t' \circ f_A
\end{eqnarray*}
である。

それでは冒頭で示した例を用いて終対象を求める。グラフそのものを用いたほうが分かりやすいので、その推移を示したのが下図である。

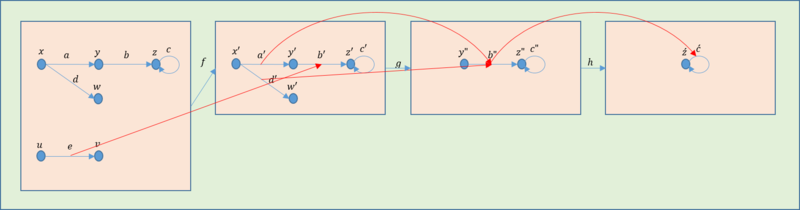
これを圏として表すと次のようになる。

ここで、
\begin{eqnarray*}
f_N \circ s & = & s' \circ f_A \\
f_N \circ t & = & t' \circ f_A \\
g_N \circ s' & = & s" \circ g_A \\
g_N \circ t' & = & t" \circ g_A \\
h_N \circ s" & = & \acute{s} \circ h_A \\
h_N \circ t" & = & \acute{s} \circ h_A
\end{eqnarray*}
が満足されていることに注意してほしい。