1.集合内の写像
集合間の写像を学んだので、集合内の写像がどのようになっているかを観察してみる。集合内の写像は、特別に、endomapと呼ばれる。
前回の記事で紹介した集合間の全ての写像を求める関数mapping m nは次のようになっていた。
module Mapping where mapping' :: a -> [b] -> [(a,b)] mapping' y n = map (\x -> (y,x)) n mapping :: [a] -> [b] -> [[(a,b)]] mapping [] _ = [[]] mapping (m:mx) n = [[x] ++ y | x <- (mapping' m n), y <- (mapping mx n)]
集合内の写像の全ての集まりを求める関数をendomapとする。集合内の写像は、写像する側と写像される側の集合が同一である。従って、mappingの二つの引数を同一にして、次のように表すことができる。
endomap m = mapping m m
例えば、集合を\(A=\{a,b,c\}\)とした時、この集合内での写像の集合は以下のようになる。
*Mapping> endomap ['a'..'c'] [[('a','a'),('b','a'),('c','a')],[('a','a'),('b','a'),('c','b')],[('a','a'),('b','a'),('c','c')],[('a','a'),('b','b'),('c','a')],[('a','a'),('b','b'),('c','b')],[('a','a'),('b','b'),('c','c')],[('a','a'),('b','c'),('c','a')],[('a','a'),('b','c'),('c','b')],[('a','a'),('b','c'),('c','c')],[('a','b'),('b','a'),('c','a')],[('a','b'),('b','a'),('c','b')],[('a','b'),('b','a'),('c','c')],[('a','b'),('b','b'),('c','a')],[('a','b'),('b','b'),('c','b')],[('a','b'),('b','b'),('c','c')],[('a','b'),('b','c'),('c','a')],[('a','b'),('b','c'),('c','b')],[('a','b'),('b','c'),('c','c')],[('a','c'),('b','a'),('c','a')],[('a','c'),('b','a'),('c','b')],[('a','c'),('b','a'),('c','c')],[('a','c'),('b','b'),('c','a')],[('a','c'),('b','b'),('c','b')],[('a','c'),('b','b'),('c','c')],[('a','c'),('b','c'),('c','a')],[('a','c'),('b','c'),('c','b')],[('a','c'),('b','c'),('c','c')]]
全てで27個の写像があるが、この中には、名前を入れ替えると同じ写像になるものがいくつかある。そこで、名前を入れ替えたときに同じ写像になるものについては、そのうちの一つだけを選ぶようにすると、構造が異なる写像は以下のようになる。

上の図で、写像する側と写像される側の対象を一緒にすると次のようになる。

上の図で、複数の離れた島で構成されているのが、\(f_1,f_2,f_5\)である。このうち、\(f_1\)は自分自身へ移す写像であるため、恒等写像である。写像によってすべてがつながっているのが、\(f_3,f_4,f_6\)である。このうち、\(f_6\)はループになっている。
2.集合内の写像より圏を作成
上の図の6個の写像のそれぞれに対して圏を作成することを考える。対象は集合\(A=\{a,b,c\}\)とし、射は写像とする。また、圏にするために、それぞれに恒等写像を恒等射として加えるとともに、射の合成も含めることにする。このようにして、それぞれに圏を作成すると以下の図のようになる。

3.始対象
前回の記事で、始対象の説明をした。それは次のようになっていた。一つの対象をすべての対象に写像するような射が丁度一つ存在するとき、写像する側の対象を始対象と呼ぶ。
集合内の写像により作られる圏に対する始対象を考えることにする。例えば、\(f_3\)で作成された圏に対して、始対象を含むような圏を下図のように考えることとする。

図で?マークで書かれている部分が求める始対象である。この始対象からは、\(f_3\)で作成された圏の全ての対象に写像する唯一つの射が存在する必要がある。集合間の写像のところで出てきたが、このような射は空集合からの空写像であった。従って、始対象は空集合となる。また、始対象から全ての対象への射は空写像となる。
空対象は図で表すと、何もないので、次のようになる(ここでは、写像付きの集合を扱っているので、始対象は、単に、空対象というよりも、空対象から空対象への空写像を有する空集合と言ったほうが正確である)。

4.終対象
前回の記事で、終対象の説明もした。それは次のようになっていた。全ての対象を一つの対象に写像するような射が丁度一つ存在するとき、写像される側の対象を終対象という。
集合内の写像により作られる圏に対する終対象を考える前に、写像(endomap)を有する集合の間での写像について考える。これは下図のようになる。

上図で、写像\(f\)は集合\(X\)から集合\(Y\)へ写像している。また、写像\(\alpha\)は集合\(X\)に与えられた写像の一つ、写像\(\beta\)は集合\(Y\)に与えられた写像の一つである。圏論での写像は、その構造を保持して移すことが要求されるので、写像を有する集合の間での\(f\)は\(f:X \rightarrow Y\)を満たすだけでなく、\(f \circ \alpha = \beta \circ f\)を満たすことが要求される。即ち、上図が可換図式となることが要求される。
準備ができたので、集合内の写像により作られる圏に対する終対象を考えることにする。例えば、\(f_3\)で作成された圏に対して、終対象を含むような圏を下図のように考えることとする。

そこで、ただ一つの要素を有し、写像は恒等射だけの、下図のような写像付き集合を考える。

\(f_3\)で作成された圏に対して、上記の写像を持つ集合を含むような圏を求めると下図のようになる。
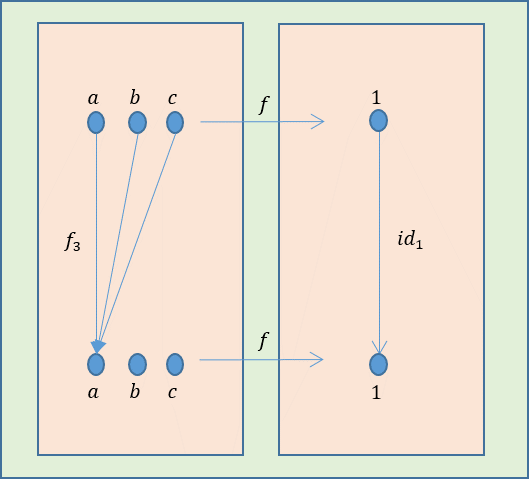
ここで、\(f\)を集合\(A=\{a,b,c\}\)から要素を一つだけ持つ集合\(1\)への写像とする。この時、\(f \circ f_3 = id_1 \circ f\)が成り立つので、\(f\)は構造を保持した写像であることが分かる。また、集合\(A\)から集合\(1\)への写像は一つしか存在しないので、\(f\)はただ一つの写像となる。これから、一つの要素で構成され、恒等射を有する集合が終対象となっていることが分かる。
このことから、集合\(A=\{a,b,c\}\)の要素はどれも恒等射を有するので、どの要素も終対象となりえることが分かる。
\(f_3\)で作成された圏はつぎのようになっている。
(1)対象:集合\(A=\{a,b,c\}\)
(2)射:\(f_3\)
(3)ドメインとコドメイン:\(f_3: A \rightarrow A\)
(4)恒等射:\(id_A : A \rightarrow A\)
(5)合成:\(f_3\)同士での合成関数、それらと終対象への写像の間での合成写像
圏のための二つの条件を満たしていることは確認して欲しい。
\(c\)を終対象とした時の圏は下図のようになる。

さらに、\(c\)を終対象として明示すると圏は次のようにあらわすことができる。
(1)対象:集合\(A=\{a,b,c\}\)と集合\(A'=\{c\}\)
(2)射:\(f_3\)と\(f\)
(3)ドメインとコドメイン:\(f_3: A \rightarrow A\)と\(f: A \rightarrow A'\)
(4)恒等射:\(id_A : A \rightarrow A\)と\(id_{A'} : A' \rightarrow A'\)
(5)合成:\(f_3\)と\(f\)からの合成関数(\(f_3\)同士も含む)
なお、終対象を\(c\)の代わりに、\(a\)としても\(b\)としても図からわかるように同型であることに注意してほしい。
上記の圏をHaskellで定義すると以下のようになる(なお、\(C\)を終対象として扱っているときは\(C'\)とした)。
data SetA = A | B | C deriving (Show, Eq) data SetOne = C' deriving (Show, Eq) mapf :: SetA -> SetOne mapf x | x == A = C' | x == B = C' | x == C = C' | otherwise = error "Unidefined source." mapf3 :: SetA -> SetA mapf3 x | x == A = A | x == B = A | x == C = A | otherwise = error "Unidefined source." idOne :: SetOne -> SetOne idOne x | x == C' = C' | otherwise = error "Unidefined source." idA :: SetA -> SetA idA x | x == A = A | x == B = B | x == C = C | otherwise = error "Unidefined source."
これを実行して、\(f \circ f_3 = id_1 \circ f\)が成り立っていることを確認する。実行結果は以下のとおりである。
*Mapping> (mapf . mapf3) A C' *Mapping> (idOne . mapf) A C' *Mapping> (mapf . mapf3) B C' *Mapping> (idOne . mapf) B C' *Mapping> (mapf . mapf3) C C' *Mapping> (idOne . mapf) C C'
ここでは、具体的な例に対して始対象と終対象を求めたが、一般に、写像を有する集合で構成される圏においては、始対象は空集合であり、終対象は1要素と恒等射を有する集合となる。
5.一般的な集合の圏と自身への写像を有する集合の圏
前回の記事では集合間の写像を、今回は集合内の写像について論じたが、両者の関係について説明しておく。前者は「集合全般」を、後者は「自分への写像endomapを有する集合」を論じるために説明した。前者の話はとっても一般的な集合についてだが、後者の話は集合に構造を持たせたものである。
そこで、一般的な集合が構成する圏と、endomapを有する集合が構成する圏とについて、それぞれの定義が一般化できるように、しかし、具体的なイメージが湧くような例で説明する。
以下の図は、集合\(A,B,C\)で構成される圏である。

この圏は以下のように構成される。
(1)対象:集合\(A=\{a_1,a_2,a_3\}\)、集合\(B=\{b_1,b_2,b_3\}\)、集合\(C=\{c_1,c_2,c_3\}\)
(2)射:写像\(f\)、写像\(g\)
(3)ドメインとコドメイン:\(f:A \rightarrow B\), \(g:B \rightarrow C\)
(4)恒等射:\(id_A : A \rightarrow A\), \(id_B : B \rightarrow B\), \(id_C : C \rightarrow C\)
(5)合成:\(f \circ g\), \(id_A \circ f\), \(f \circ id_B\), \(id_B \circ g\), \(g \circ id_C\)など
圏のための二つの条件を満たしていることは確認して欲しい。
次にこの圏に終対象を加える。終対象の集合を\(1\)とし、その要素(一つしかない)も\(1\)とする。以下の図のようになる。

また、以下のように構成される。
(1)対象:集合\(A=\{a_1,a_2,a_3\}\)、集合\(B=\{b_1,b_2,b_3\}\)、集合\(C=\{c_1,c_2,c_3\}\)、集合\(1=\{1\}\)
(2)射:写像\(f\)、写像\(g\)、写像\(h\)
(3)ドメインとコドメイン:\(f:A \rightarrow B\), \(g:B \rightarrow C\), \(h:A, B, C \rightarrow 1\)
(4)恒等射:\(id_A : A \rightarrow A\), \(id_B : B \rightarrow B\), \(id_C : C \rightarrow C\), \(id_1 : 1 \rightarrow 1\)
(5)合成:\(f \circ g\), \(id_A \circ f\), \(f \circ id_B\), \(id_B \circ g\), \(g \circ id_C\), \(f \circ id_h\), \(g \circ h\)など
それでは、endomapを有する集合について考える。上記の集合の圏に、内部の写像を加えると次のようになる。

ここで、集合\(A,B,C\)に対する内部写像はそれぞれ\(\alpha,\beta,\gamma\)である。また、endomapを有する集合の圏となる必要な条件
\begin{eqnarray*}
f \circ \alpha & = & \beta \circ f \\
g \circ \beta & = & \gamma \circ g
\end{eqnarray*}
は満たされるように、 \(f, g\)は定められているとする。
この圏は次のように構成される。
(1)対象:集合\(A=\{a_1,a_2,a_3\}\)、集合\(B=\{b_1,b_2,b_3\}\)、集合\(C=\{c_1,c_2,c_3\}\)
(2)射:写像\(f\)、写像\(g\)、写像\(\alpha\)、写像\(\beta\)、写像\(\gamma\)
(3)ドメインとコドメイン:\(f:A \rightarrow B\), \(g:B \rightarrow C\), \(\alpha:A \rightarrow A\), \(\beta:B \rightarrow B\), \(\gamma:C \rightarrow C\)
(4)恒等射:\(id_A : A \rightarrow A\), \(id_B : B \rightarrow B\), \(id_C : C \rightarrow C\)
(5)合成:\(f \circ g\), \(id_A \circ f\), \(f \circ id_B\), \(id_B \circ g\), \(g \circ id_C\), \(f \circ \alpha\), \(\beta \circ f\), \(g \circ \beta\), \(\gamma \circ g\)など
なお、圏のための二つの条件を満たしていることは確認して欲しい。
なお、この圏に終対象を加えたものは次のようになる。

6.写像連鎖の果ての終対象
終対象という言葉から、最後という意味が感じられるが、今までの話の中では、そのような感じを受けない。そこで、今度は、集合間の写像に少し制約を課すことにする。一つ目の制約は写像は全射(写像される側の全ての要素に対して写像してくる相手がいる)とする。さらに、写像される側の集合が小さくなっていくようにするため、写像する側の要素の数のほうが写像される側の要素の数よりも大きいとする。このようにすると、写像を繰り返すうちに、それ以上は辿れない集合が出てくる。これが終対象である(証明は省く)。
例を挙げると次のようになる。

上の図で、写像\(f\)は\(a_1,a_3\)を\(b_1\)に\(a_2\)を\(b_2\)に写像する。また、\(g\)は\(b_1,b_2\)を\(c_1\)に写像する。
また、
\begin{eqnarray*}
f \circ \alpha & = & \beta \circ f \\
g \circ \beta & = & \gamma \circ g
\end{eqnarray*}
が成り立っていることは確認して欲しい。