ケットとブラでの状態の表し方、そして、状態の重ね合わせも学んだので、量子力学の世界を少しだけ垣間見ることにしよう。
3年前の秋(2013年)に情報科学・工学関連の学会が鳥取大学で開催された。修士の学生が発表したのだが、彼の発表の合間を利用して、鳥取砂丘を訪れた。台風が通り過ぎた後で、すさまじい風が吹いていて、砂丘では、多量の砂が飛散していた。たくさんの砂が飛び散っているにもかかわらず、(平行移動しているかもしれないが)砂丘の形が変わらないのは、現象として興味深かった。飛び散った砂粒の後に、他の場所からそれを補う砂粒が移ってくるのだろう。

今回はこれに似たような現象を量子力学の世界で考えてみよう。
粒子が飛び交っている世界、何で表したらよいであろうか。一つは時間だ。時間とともに、砂粒が移動しているので、それを上手に表すことが必要になる。粒子の移動はどのように表したらよいであろうか。時間ごとの位置というのもある。しかし、これらは、それぞれの粒子の位置を表さなければならないので大変そうである。
もし、粒子が等速運動をしていると仮定したらどうであろうか。個々の粒子に共通する速度で現象を表すことができるようになる。それでは速度はどのように表したらよいであろうか。我々が手に入れている道具は、生成演算子と消滅演算子である。単位時間の間に作用する生成演算子と消滅演算子の列を粒子が移動する速度ととらえてはどうであろうか。
冒頭の話では、粒子は飛んでいるけれども、砂丘の形は変わっていないという話をした。そこで、単位時間の中で、隣り合う場所にある粒子が入れ替わるという単純なモデルを考えてみることにしよう。これであれば、それぞれの格子点で観察される粒子の数は変化しないので、砂丘の形が変わらないのと似たような現象を見ることができるかもしれない。
1.粒子が相互に交換されるモデル
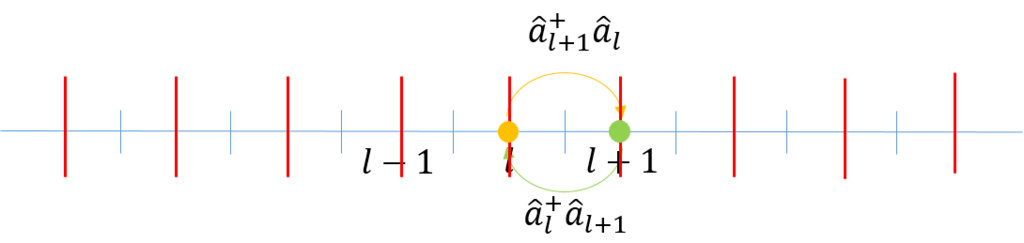
それでは隣り合う格子点の間で粒子が相互に交換されるモデルを考えることとする。モデルは図のようになる。図で上の矢印は、\(l\)番目の格子点から\(l+1\)番目の格子点へ1粒子が移る姿を示した。具体的には、\(l\)番目の格子点で消滅演算子が作用し、それに引き続いて、\(l+1\)番目の格子点で生成演算子が作用する。図の下の矢印はこれとは反対である。
今、1粒子状態の重なり合いを考える。重ね合わせは時間\(t\)とともに変化するものとし、\( \hat{\Psi}\),\( \hat{\psi}_l\)は\(t\)の関数とする。そこで、1粒子の状態を例によって次のように表す。なお、\( \hat{\Psi}(t)\)は規格化されているとする。
\( \hat{\Psi}(t) = \sum_{l=-\infty}^\infty \psi_l(t) \hat{a}^\dagger_l|0> \)
今、\( \hat{\Psi}(t)\)を状態であることを強調するために、\( \hat{\Psi}(t)=|\Psi(t)>\)と表すことにしよう。
微小時間\(dt\)での、状態の移動量は次のようになる。
\begin{align*}
& \sum_{l=-\infty}^\infty (\hat{a}^\dagger_{l+1} \hat{a}_l + \hat{a}^\dagger_{l} \hat{a}_{l+1}) | \Psi(t)> \\
=& \sum_{l=-\infty}^\infty (\psi_{l-1}(t)+\psi_{l+1}(t))\hat{a}^\dagger_{l}|0>
\end{align*}
状態を微分したものは、係数が異なるだけで状態の移動量と同じになる。即ち、
\begin{align*}
&\frac{d}{dt} |\Psi(t)> \\
=& \alpha \sum_{l=-\infty}^\infty (\hat{a}^\dagger_{l+1} \hat{a}_l + \hat{a}^\dagger_{l} \hat{a}_{l+1}) | \Psi(t)> \\
=& \alpha \sum_{l=-\infty}^\infty (\psi_{l-1}(t)+\psi_{l+1}(t))\hat{a}^\dagger_{l}|0>
\end{align*}
上の式を一般化しよう。微小時間\(dt\)での、粒子への作用を\(\hat{H}\)で表すことにしよう。これはハミルトニアンと呼ばれる。一般に、重ね合わせの状態\(|\Psi(t)>\)を微分したものは、この状態にハミルトニアン\(\hat{H}\)で与えられる作用を施したものに、係数\(\alpha\)倍だけ異なる。即ち、
\(\frac{d}{dt}|\Psi(t)>=\alpha \hat{H}|\Psi(t)>\)
となる。なお、\(|\Psi(t)>\)は、重ね合わせ状態である。従って、これまで話を進めている1粒子状態に限らず、一つの格子点に複数の粒子が存在する場合も含んでいる。
一般に量子力学では係数を次のように定めている。
\(i \hbar \frac{d}{dt}|\Psi(t)>=\hat{H}|\Psi(t)>\)
ここで、\(\hbar\)はディラック定数と呼ばれる。\(\hbar\)は、\(1.054571...\times 10^{-34} \ J \ sec\)で、\(J \ sec\)は\(Kg \ m^2 /sec\)である。
隣り合う格子点の間で粒子が相互に移動するモデルでは
\(\hat{H}=-g\sum_{l=-\infty}^\infty (\hat{a}^\dagger_{l+1} \hat{a}_l + \hat{a}^\dagger_{l} \hat{a}_{l+1})\)
として計算しよう。これより、
\( i \hbar \frac{d}{dt}\psi_m(t) = -g [\psi_{m -1}(t) + \psi_{m+1}(t)] \)
を得る。
2.定常解を求める
方程式
\( l \hbar \frac{d}{dt}\psi_m(t) = -g [\psi_{m -1}(t) + \psi_{m+1}(t)]\)
を得ることができたので、これの解を求めることにしよう。取り敢えず、定常解を求めることにする。
専門用語を説明する必要がある。定常解の前提となるのが定常状態だ。これは、任意の演算子\(\hat{O}\)に対して、\(<\Psi(t)|\hat{O}|\Psi(t)>\)が時間\(t\)に依存しない場合、状態\(|\Psi(t)>\)を定常状態と呼ぶ。このとき、
定常状態\(|\Psi(t)>\)が
\(i \hbar \frac{d}{dt}|\Psi(t)>=\hat{H}|\Psi(t)>\)
の解であるとき定常解という。
1粒子状態のときは、粒子が\(l\)番目の格子点で発見される確率\(P_l(t)=\psi^*_l(t)\psi_l(t)\)が時間に依存しないとき、
\(\psi_l(t)\)が
\( i \hbar \frac{d}{dt}\psi_m(t) = -g [\psi_{m -1}(t) + \psi_{m+1}(t)]\)
の定常解である。
定常解はいくつかあるが、その一つは、
\(\psi_l(t) = Ae^{-i \omega t+ i \kappa l}\)
である。但し、\(\hbar \omega= -2g \cos \kappa \)である。また、\(\omega\)は角振動数と呼ばれる。\(\kappa\)は1格子点間の間での位相差である。\(d\)を格子点間の長さとすると、\(\frac{2\pi}{\kappa}\times d = \lambda\)(波長)である。\(k = \kappa / d\)は波数と呼ばれる。
定常解であることは、下記の式
\(\psi^*_l(t)\psi_l(t) = A^* e^{i \omega t- i \kappa l}Ae^{-i \omega t+ i \kappa l}=A^*A=|A|^2 \)
が時間\(t\)に寄らないことから明らかである。
\(\psi_l(t) = Ae^{-i \omega t+ i \kappa l}\)がどのようなものかをイメージさせてくれるのがスクリューである(fukutiの製品紹介から借用させてもらう)。スクリューは角振動数\(\omega\)で回転し、その刃のピッチは格子点間での位相差が\(\kappa\)となるように刻まれている。スクリューの刃先が\(\psi_l(t)\)を表しているといえる。なお、図で横方向が格子点の並びを表し、縦方向が\(\psi_l(t)\)の実数部、奥行方向が虚数部である。

それでは上記のスクリューを図に垂直方向に切断してその断面を見てみよう。
\(t=0\)の時は、次のようになっている。なお、下図で、上の部分が断面図、下の部分は、解の実数部を描いたものである(刃先を壁面に投影したもの)。

解の実数部を見ると、コサインのカーブをがいていることが分かる。
次の図は、\(\omega\)だけ進んだ\(t=t'\)の時の断面図と解の実数部を描いたものである。

解が無限な領域であるので、プログラムでは表現しにくい。そこで、次回は、区間を有限にし、Haskellの世界で描写することにしよう。
そろそろ梅雨も明けそうなので、明日から一週間ハワイで休養する。その間に、有限な区間での量子力学の世界を考えることとする。