8.ボーズ粒子とフェルミ粒子
粒子には二つの種類がある。一つは、光子に代表されるボーズ粒子であり、他の一つは、電子を代表とするフェルミ粒子である。
ボーズ粒子が来るものは拒まずというような性質を有しているのに対して、フェルミ粒子は共存はできないという性格を持っている。
このような性質はどこから来るのであろうか。
今、二つの粒子\(a\),\(b\)があるとし、その位置を入れ替えることにしよう。入れ替える前の状態を\(|source>\)、後の状態を\(|target>\)で表すことにしよう。入れ替えるときの演算子を\(P\)とすると
\begin{eqnarray}
| target> = P | source>
\end{eqnarray}
となる。また、これを具体的に図で示すと

なお、\(|source>=\hat{a}^\dagger_l \hat{a}^\dagger_k |0>\)で、\(|target>=\hat{a}^\dagger_k \hat{a}^\dagger_l |0>\)とする。即ち、\(a\)が発生演算子\(\hat{a}^\dagger_k\)によって格子点番号\(k\)に先に入り、\(b\)が\(\hat{a}^\dagger_l\)によって\(l\)に後で入って、状態\(|source>\)が作られたとする。さらに、\(a\)が\(\hat{a}^\dagger_l\)によって、\(l\)に先に入り、\(b\)が\(\hat{a}^\dagger_k\)によって\(k\)に後で入って、状態\(|target>\)が作られたとする。
また、\(|source>\)から\(|target>\)へは、次図のように、一つずつ粒子を移動させて得ることができる。
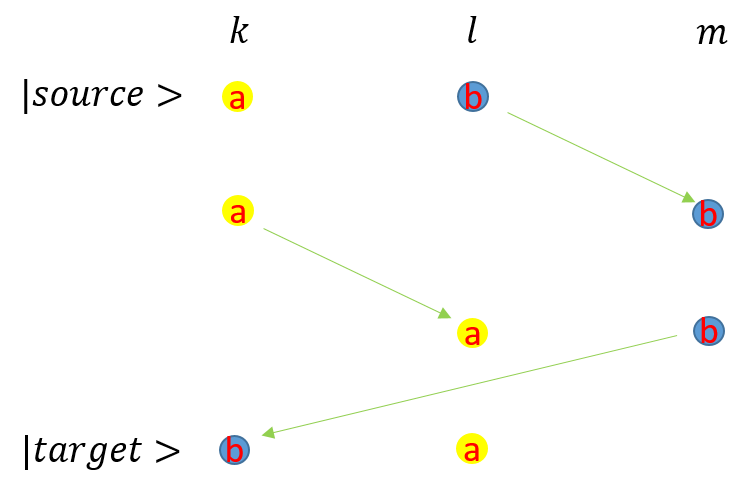
この状態でもう一度入れ替えると、
\begin{eqnarray}
|source> = P |target> = P^2 |source>
\end{eqnarray}
となる。そこで、そこで上の式を満たす\(P\)は\(1\)あるいは\(-1\)となる。
これから、\(P\)の値によって二種類の粒子が存在することが分かるが、結論から言うと、\(P=1\)の場合がボーズ粒子であり、\(P=-1\)がフェルミ粒子である。そこで、この性質は、生成演算子同士、消滅演算子同士、あるいは生成演算子と消滅演算子の順序に由来していると考えてみよう。
そして、それぞれの粒子について、演算子の交換法則を定義してみよう。
8.1 ボーズ粒子
まず、ボーズ粒子から話を始めよう。\(P=1\)から演算子の順序を交換しても変わらないとし、次のことが成り立っていると考える。
二つの生成演算子\(\hat{a}^\dagger_k\)と\(\hat{a}^\dagger_l\)については、交換しても変わらないとする。即ち、
\begin{eqnarray}
\hat{a}^\dagger_k \hat{a}^\dagger_l= \hat{a}^\dagger_l \hat{a}^\dagger_k
\end{eqnarray}
二つの消滅演算子\(\hat{a}^\dagger_k\)と\(\hat{a}^\dagger_l\)についても、交換しても変わらないとする。
\begin{eqnarray}
\hat{a}^\dagger_k \hat{a}^\dagger_l = \hat{a}^\dagger_l \hat{a}^\dagger_k
\end{eqnarray}
消滅演算子\(\hat{a}_k\)と生成演算子\(\hat{a}^\dagger_l\)については、\(k \neq l\)の時は、交換しても変わらないとする。即ち、
\begin{eqnarray}
\hat{a}_k \hat{a}^\dagger_l = \hat{a}^\dagger_l \hat{a}_k
\end{eqnarray}
また、\(k = l\)の時は、生成させた後に消滅させることになる。これは何もしなかったことと同じなので、1ということにする。
\begin{eqnarray}
\hat{a}_k \hat{a}^\dagger_l= 1
\end{eqnarray}
そこで、
\begin{eqnarray}
\hat{a}^\dagger_l \hat{a}_l = 0
\end{eqnarray}
を考慮すると、
\begin{eqnarray}
\hat{a}_k \hat{a}^\dagger_l = \delta_{kl} + \hat{a}^\dagger_l \hat{a}_k
\end{eqnarray}
となる。なお、\(\delta_{kl}\)はδ関数で、\(k = l\)の時は\(1\)、\(k \neq l\)の時は\(0\)である。
交換カッコ\([\hat{A},\hat{B}]=\hat{A},\hat{B}-\hat{B},\hat{A}\)を用いると、上記の式は
\begin{eqnarray}
[\hat{a}^\dagger_k \hat{a}^\dagger_l] &=& \hat{a}^\dagger_l \hat{a}_l = 0 \\
[\hat{a}^\dagger_k \hat{a}^\dagger_l] &=& \hat{a}^\dagger_l \hat{a}^\dagger_k = 0 \\
[\hat{a}_k \hat{a}^\dagger_l] &=& \delta_{kl}
\end{eqnarray}
となる。
8.2 フェルミ粒子
次に、フェルミ粒子に移ろう。\(P=-1\)から順序を変えると変わってしまうと考え、次のことが成り立っていると考える。
二つの生成演算子\(\hat{c}^\dagger_k\)と\(\hat{c}^\dagger_l\)については、符号が変わるとする。即ち、
\begin{eqnarray}
\hat{c}^\dagger_k \hat{c}^\dagger_l= -\hat{c}^\dagger_l \hat{c}^\dagger_k
\end{eqnarray}
但し、\(k = l\)の時は、
\begin{eqnarray}
\hat{c}^\dagger_k \hat{c}^\dagger_k= -\hat{c}^\dagger_k \hat{c}^\dagger_k
\end{eqnarray}
となる。これを満足するのは、\(\hat{c}^\dagger_k \hat{c}^\dagger_k=0\)の時だけである。このことから、フェルミ粒子は、同じ場所では、複数が同時に存在できないということになる。
二つの消滅演算子\(\hat{c}^\dagger_k\)と\(\hat{c}^\dagger_l\)についても、符号が変わるとする。
\begin{eqnarray}
\hat{c}^\dagger_k \hat{c}^\dagger_l= -\hat{c}^\dagger_l \hat{c}^\dagger_k
\end{eqnarray}
消滅演算子\(\hat{c}_k\)と生成演算子\(\hat{c}^\dagger_l\)については、\(k \neq l\)の時は、符号が変わるとする。即ち、
\begin{eqnarray}
\hat{c}_k \hat{c}^\dagger_l= -\hat{c}^\dagger_l \hat{c}_k
\end{eqnarray}
また、\(k = l\)の時は、生成させた後に消滅させることになる。これは、ボーズ粒子の時と同様に、何もしなかったことと同じなので、1ということにする。
\begin{eqnarray}
\hat{c}_k \hat{c}^\dagger_l= 1
\end{eqnarray}
そこで、前と同じように、
\begin{eqnarray}
\hat{c}^\dagger_l \hat{c}_l = 0
\end{eqnarray}
を考慮すると、
\begin{eqnarray}
\hat{c}_k \hat{c}^\dagger_l = \delta_{kl} - \hat{c}^\dagger_l \hat{c}_k
\end{eqnarray}
となる。
反交換カッコ\({\hat{c},\hat{B}}=\hat{A},\hat{B}+\hat{B},\hat{c}\)を用いると、上記の式は
\begin{eqnarray}
{\hat{c}^\dagger_k \hat{c}^\dagger_l} &=& \hat{c}^\dagger_l \hat{c}_l = 0 \\
{\hat{c}^\dagger_k \hat{c}^\dagger_l} &=& \hat{c}^\dagger_l \hat{c}^\dagger_k = 0 \\
{\hat{c}_k \hat{c}^\dagger_l} &=& \delta_{kl}
\end{eqnarray}
となる。