この3月に退職して以来、これまで専門としてきた情報科学の研究から離れて、日本の古代史(平安時代の終わりまで)を勉強している。
僕が高校生だった頃は、社会科の科目には、社会、世界史、日本史、地理の4科目が設けられていた。その内で、社会は必修で、残りの3科目の中から2科目を選択し、合わせて3科目を学習するようになっていた。
僕が入学したいと思っていた大学は、社会は受験科目に含まれておらず、世界史、日本史、地理の中から2科目を選んで受験することとなっていた。もともと地理は好きだったので、中学生の頃にはかなりのことが身についていて、そのまま、大学受験をしても大丈夫な程度の知識を有していた。このため、知識の量を増やすという観点に立てば、世界史と日本史を選択して高校時代を過ごせばよかったのだが、大学へ入学できることを最優先にして、高校では、地理と世界史を学んだ。そのため、日本史を学ぶ機会を失ってしまったため、この歳になって学びなおしてみたいと思うようになった。
幸いなことに、古代史の研究は、新たな遺跡の発見や発掘などの恩恵もあって、近年、大きな変貌を遂げている。もし、高校時代に学んでいたとすると、その時の知識が邪魔をして、今日の新しい考え方が素直に入ってこなかったのではないかと思い、変な意味で、高校時代に日本史を学ばなかったことに今感謝している。
しかし、新しい分野を学ぶということは大変なことで、頭の中にその分野の体系を形作るまでに、受験勉強にも勝る努力を必要とする。最近は、インターネットのおかげでとても便利な世の中になり、分からないことがあった時には、図書館を訪れるまでもなく、ウィキペディアで調べれば、瞬時に情報を得ることができる。知りたいと思っていた情報を得ることがかくも簡単になったので、学ばなくてもいいのだという暴言を吐く人もいるようだが、それに関連する知識をある程度有していないと、折角、情報を得たとしてもそれを理解することはできない。
ウィキペディアを利用するときは、それを確認するときという程度にまでなっていれば、その分野についての体系が頭の中にちゃんと構成されているのだろうと思う。この状態をめざして、そろそろ、半年になるが、勉強を続けている。
さて、勉強の仕方だ。一つは専門家から教えてもらった方が、良いだろうということで、カルチャセンターを利用して、古代史の専門家の講義を聞いている。専門家はその分野のツボを心得ているので、何となく言った言葉に深い知見が含まれていることが時々ある。沢山の知識を持っている素人の研究家と専門家の違いは、学問の核心を知っているかどうかだと思うが、その違いがちょっとした話の中に出てくることが多い。その意味では、その分野で業績を上げている人の話を聞くことは欠かすことができない。
二つ目は乱読である。その分野についての体系を得るためには、できるだけ、沢山の本を読んで、その概略を知ることが必要だと考えている。その時、あまり細かいことを気にする必要がない。自分の中で、大雑把なストーリーを構成していくのがよい。
沢山の本を読むことになるので、全ての本を購入したのでは費用もかさむし、その中に、欲しくない本も紛れ込むことになる。そこで、図書館を利用することを勧める。住んでいる市が小さいとそこの図書館で読みたいと思う本を見つけ出すことは大変だろうと思うが、幸い、僕の住んでいるところは人口が40万人の中規模な市なので、図書館の蔵書数もそれなりにある。このため、読みたいなと思った本が手に入る可能性は高い。4月から図書館の利用を始めたが、借りた本は15冊程度になっている。
もっとも、本当に良さそうな本は、電子書籍で購入しているので、すでに古代史の関連の本は25冊を超えて読んでいるものと思う。これだけ読むと、どの著者の本を読めばよいかが自ずと分かってくる。幸いに、カルチャーセンターでの先生は、『権記』、『御堂関白記』、最近では『小右記』の現代語訳を出版するなど、精力的に研究を行っている方で、優れた専門家の一人であることが分かった。
三つ目は精読なのだが、まだ、この段階には入っていない。
さて、古代史を勉強する傍らで、量子力学をHaskellで表現する作業を続けている。時間を見つけての仕事となるので、飛び飛びになってしまう。前回は、発生演算子と消滅演算子を連続系で表現したので、今回は、これを用いて、ハミルトニアンの利用法を考えてみよう。
11.ハミルトニアンの活用
0)予備知識
1粒子状態で粒子を発見する確率を表す波動関数を\(\psi(x)\)で表すことにしよう。そして、これは規格化されているとする。即ち\(\psi(x)\psi^*(x)=1\)と仮定することにしよう。粒子の位置\(x\)を、粒子が発見される場所の平均値\(< x >\)で表すことにする。この時、\(< x >\)は、次の式で表すことができる。
\begin{eqnarray}
< x > = \int^{\infty}_{-\infty} \psi^*(x) x \psi(x)dx = \int^{\infty}_{-\infty} \rho (x) x dx
\end{eqnarray}
今、\(\rho (x)\)は確率密度関数と呼ばれるが、これがが次のガウス関数であったとしよう。
\begin{eqnarray}
\rho (x) = |A|^2 e ^{-x^2/D^2} \\
A=\frac{1}{\sqrt{D \sqrt{}\pi}}
\end{eqnarray}
このとき、粒子の位置は次のようになる。
\begin{eqnarray}
\int^{\infty}_{-\infty} |A|^2 e ^{-x^2/D^2} x dx = 0
\end{eqnarray}
なお、ガウス関数は次の図のように釣り鐘型をしており、\(\rho (x)\)は\(x=0\)で最大となり、\(x\)の絶対値が大きくなるとどんどん0に近付く。
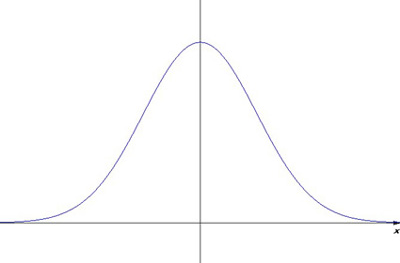
粒子の位置は\(x\)で、運動量は\(p=\hbar k\)、運動エネルギーは\(E=\frac{p^2}{2m}=\hbar \omega\)で表わさる。そこで、これらの平均値を考えることにしよう。
1) 位置を表す演算子
今、演算子\(\hat{X}\)を次のように定義しよう。
\begin{eqnarray}
\hat{X} = \int^{\infty}_{-\infty} x \hat{a}^\dagger(x) \hat{a}(x) dx
\end{eqnarray}
\(\hat{X}\)を\(\hat{a}^\dagger(x')|0>\)に作用させると
\begin{eqnarray}
&&\hat{X}\hat{a}^\dagger(x')|0> \\
&=& \int^{\infty}_{-\infty}[ x \hat{a}^\dagger(x) \hat{a}(x)] \hat{a}^\dagger(x') dx |0> \\
&=& \int^{\infty}_{-\infty} x \hat{a}^\dagger(x) [\hat{a}(x) \hat{a}^\dagger(x')] dx |0> \\
&=& \int^{\infty}_{-\infty} x \hat{a}^\dagger(x) \delta(x-x')] dx |0> \\
&=& x' \hat{a}^\dagger(x') |0>
\end{eqnarray}
となるので、\(\hat{a}^\dagger(x')|0>\)は、\(\hat{X}\)の固有状態であり、その固有値は\(x'\)である。
そこで、\(\hat{X}\)を1粒子状態の重ね合わせ\(\int^{\infty}_{-\infty} \psi (x) \hat{a}^\dagger(x) |0> dx \)に作用させると
\begin{eqnarray}
\hat{X} \int^{\infty}_{-\infty} \psi (x) \hat{a}^\dagger(x) |0> dx = \int^{\infty}_{-\infty} \psi (x) x \hat{a}^\dagger(x) |0> dx
\end{eqnarray}
となる。これより、\(\psi (x)\)が規格化された波動関数である時、
\begin{eqnarray}
< \hat{X} > = \left[ < 0 | \int^{\infty}_{-\infty} \psi^* (x) \hat{a}(x) dx \right] \hat{X} \left[ \int^{\infty}_{-\infty} \psi (x') \hat{a}^\dagger(x') dx' |0>\right] = 0
\end{eqnarray}
となり、\(\hat{X} = \int^{\infty}_{-\infty} x \hat{a}^\dagger(x) \hat{a}(x) dx\)が位置を表す演算子であることが分かる。
なお、詳しい式の展開を知りたいときは、西野友年著『場の理論』を参考にして欲しい。以下同じである。
2)運動量を表す演算子
1粒子の運動量は、波数\(k\)を用いると、\(\hbar k\)となる。そこで、位置の平均値を求めた時と同じように、運動量の平均値を求めるために、\(x\)のところを\(\hbar k\)で置き換えて、次のような演算子を用意しよう。
\begin{eqnarray}
\hat{P} = \int^{\infty}_{-\infty} \hbar k \hat{a}^\dagger(k) \hat{a}(k) dk
\end{eqnarray}
そこで、前と同じように、\(<\hat{P}>\)を考えてみよう。なお、波数の空間での規格化された波動関数を\(\phi (k)\)とする。
\begin{eqnarray}
< \hat{P} > = \left[ < 0 | \int^{\infty}_{-\infty} \phi^* (k) \hat{a}(k) dk \right] \hat{P} \left[ \int^{\infty}_{-\infty} \phi (k') \hat{a}^\dagger(k') dk' |0>\right]
\end{eqnarray}
式を変形すると
\begin{eqnarray}
< \hat{P} > = <\hbar k>
\end{eqnarray}
となる。詳しくは、西野友年著『場の理論』を参考にして欲しい。
また、波数空間ではなく、実空間を用いて表すこともできる。この時は、
\begin{eqnarray}
\hat{P} = \int^{\infty}_{-\infty} \hat{a}^\dagger(x) \left[ -i \hbar \frac{d}{dx} \right] \hat{a}(x) dx
\end{eqnarray}
となる。
また、波数空間での波動関数を以下に示すガウス関数であると仮定する。
\begin{eqnarray}
\phi(k') = A D e^{- D^2 (k - k')^2 / 2 } = \phi^*(k')
\end{eqnarray}
この時、運動量の平均値は
\begin{eqnarray}
< \hat{p} > = \hbar k
\end{eqnarray}
となる。
3)運動エネルギーを表す演算子
1粒子を取り上げてきたので、今度は、2粒子の場合を取り上げてみることにしよう。複数の粒子がある場合には、ボーズ粒子であるのかフェルミ粒子であるのかが問題になる。ここでは、フェルミ粒子としよう。長さが\(L\)でポテンシャルが存在せず、運動エネルギーだけが存在する場合を考えることにしよう。運動エネルギーは\(E=\frac{p^2}{2m}=\frac{{(hk)}^2}{2m}\)で表すことができる。また、また、長さが有限な値\(L\)とすると、波数は有限個の異なる整数となる。このため、波数については積分ではなく、和となる。このことに注意して、位置を求めた時の演算子と同じように、次の演算子\(\hat{H}\)を定義する。
\begin{eqnarray}
&&\hat{H} == \displaystyle \sum_k \frac{(\hbar k)^2}{2m}\hat{c}^\dagger_k \hat{c}_k
\end{eqnarray}
二つの粒子が波数\(k_1\)と\(k_1\)を有する場合の状態\( \hat{c}^\dagger_{k_1} \hat{c}^\dagger_{k_2} | 0> \)にこの演算子を作用させてみよう。
\begin{eqnarray}
&&\left[\displaystyle \sum_k \frac{(\hbar k)^2}{2m}\hat{c}^\dagger_k \hat{c}_k \right] \hat{c}^\dagger_{k_1} \hat{c}^\dagger_{k_2} | 0> \\
&=& \left[\frac{(\hbar k_1)^2}{2m}+\frac{(\hbar k_2)^2}{2m} \right] \hat{c}^\dagger_{k_1} \hat{c}^\dagger_{k_2} | 0>
\end{eqnarray}
これから、それぞれの粒子のエネルギーの和となることが分かる。
有限の長さの時は、波数が離散的になるので、これまで展開してきた離散的なモデルでのHaskellを用いて、表現することができる。
2粒子状態に対する波動関数は、スレーター行列式で表すことができるが、これについては、西野友年著『場の理論』を参考にして欲しい。