4.7 C++プログラムから圏を作成する(続き)
前回の記事で、曜日を進めるプログラムの開発状況を手順を追いながら、説明した。このプログラムは、曜日を進める関数\(increase\)と遅らせる関数\(decrease\)から出発した。最初に作った関数は、値をどこにも記憶しない純粋な関数の集まりであった。
しかし、新たな要求が発生したために、呼ばれた関数をログとして出力することが要求された。最初に最も安易な実現方法を示した。それは、グローバル変数にログを記憶するというものであった。プログラム開発に馴染んでいない初心者が陥りやすいミスの一つだが、プログラムを開発するときに心掛けなければならない参照の局所性を犯している。これは重大な欠陥で、一つの事項の変更がプログラムのあちらこちらの変更に砂がるため、後々のプログラムの改変を困難なものにしてしまう。
上記の問題を改善するために、ログを局所変数化して、それを、関数の引数で引き渡すようにした。プログラムは、随分と改善されたのだが、しかし、引数として渡された変数は、その関数での直接的な関心事ではない。恐らく、プログラムが完成してからしばらくたつと、その変数がなぜ渡されてきたのだろうと疑問に思うことになるだろう。これは、関心の分離というもう一つのプログラム開発に当たって注意しなければならない事項を無視していたために生じた。
そこで、それぞれの関数は、不必要なものは一切有しない純粋な関数にして、関数の合成で、要求仕様の変更に対応した。この時の説明で変だなと思った人も多かったのではないかと思う。数学の力が強い人なのだろうと推察する。二つの関数\(f:a \rightarrow b,g:b \rightarrow c\)があった時、それらの関数の合成は、\(h=g \circ f : a \rightarrow c\)である。
これは、プログラムでは次のようになる。
function<c(a)> h(function<b(a)> f, function<c(b)> g) {}
ところが、関数の合成は次のようになっていた。
function<pair<int, string>(int)> compose(function<pair<int, string>(int)> f, function<pair<int, string>(int)> g) { return [f, g](int x) { auto p1 = f(x); auto p2 = g(p1.first); return make_pair(p2.first, p1.second + p2.second); }; }
必要なところだけを切り出すと、\(f: int \rightarrow (Int,String), \ g: int \rightarrow (Int,String) \)となっている。
圏論での約束は、\(f\)のコドメインと\(g\)のドメインが一致していなければならないと謳っている。しかし、\(f\)のコドメインは\((Int,String)\)であるにもかかわらず、\(g\)のドメインは\(Int\)である。一致していない。このようなものを、どのようにして合成するのかという疑問がわく。これは、正しい疑問である。
3)クライスリ圏
数学は、公式に縛られる窮屈な世界だと思っている人も多いと思う。実は、そんなことはない。少し、例外的なものが発生したときは、それを含むように、概念を拡張してあげればよい。それによって、新しい体系の数学を作ることができる。
今回の場合も同じようなものだ。\(g\)のドメインは\(Int\)だ。\(f\)のコドメインには\(Int\)が含まれているので、これを利用して、射を合成できるように規則を拡張したらどうだろうかという発想が生まれる。
例えば、二つの対象\(A,B\)に対して(射\(f\)は元々は\(f: A \rightarrow B\)であったのだが)、何らかの要請で、\(f: A \rightarrow (B, C)\)とする必要が発生した。そこで、圏論での約束を少し緩めて、二つの対象\(A,B\)にして、射\(f: A \rightarrow (B, C)\)を射として認めるようにしたらどうであろうか。
この例で行くと、\(increase\)は、元々、\(Int\)から\(Int\)への関数であった。\(decrease\)も同じである。しかし、ログを作成できるようにという要求に合わせるために、これらは\(Int\)から\((Int, String)\)への関数へと変化した。
曜日を進めるプログラムがどのような圏になるかを直感的に理解してもらうために、まず、図を見てもらおう。

そこで、\(increase\)のドメインを\(Int\)とし、整数(曜日)と文字列の対であるコドメインを\(\mathcal{M}(Int)\)で表すこととしよう。即ち、\(increase:Int \rightarrow \mathcal{M}(Int)\)とする。\(decrease,stay\)についても同様である。
そこで、これらの関数は合成するときは、\(\mathcal{M}(Int)\)を\(Int\)に変換する必要がある。関数の合成にはこの機能を持たせることにしよう。そうすると、\(compose(increase,decrease)\)は、図に示したように、\(increase\)を実行した後で、\(decompose\)を実行し、最後に\(decrease\)を実行すると読むことができるので、これらの、ドメインとコドメインの関係は
\begin{eqnarray}
increase: Int \rightarrow \mathcal{M}(Int) \\
compose: \mathcal{M}(Int) \rightarrow Int \\
decrease: Int \rightarrow \mathcal{M}(Int)
\end{eqnarray}
となり、関数の合成に関する約束(合成される関数のコドメインと合成する関数のドメインは一致する)を守ることができる。
次のstayの関数について考えよう。この関数は恒等射と考えているので、入力された曜日はそのままである。またこれまでに実行してきた関数の列に対しても変化を加えてはいけないので、ここでは関数の名前\("stay"\)を出力するのではなく、空の文字列""を出力する。
圏の形になってきたので、その構成を示そう。
1) 対象:\(Day=\{0,1,2,3,4,5,6\}\)
2) 射:\(increase, decrease\)
3) ドメイン:\(Day\)、コドメイン:\(\mathcal{M}(Day)\)
4) 恒等射:\(stay\)
5) 合成:\(compose\)
① 結合律:満足
② 単位律:満足
結合律、単位律は、プログラムの内容から満たされていると判断できるが、念のため、正しいかどうか調べてみよう。次のような\(main\)のプログラムを作成して検査してみることにした。
最初の2行は恒等射となっている\(stay\)に関するものである。次の4行は、\(compose\)の実行順序によらないことを示すために、左側から実行する場合とそれとは逆の場合で変化が生じるかを調べるものである。
int main() { auto h = compose(stay, decrease); auto k = compose(decrease, stay); auto p = compose(decrease, compose(increase, decrease)); auto r = compose(compose(decrease, increase), decrease); auto s = compose(decrease, compose(decrease, compose(increase, decrease))); auto t = compose(compose(compose(decrease, decrease), increase), decrease); auto a = h(3); auto b = k(3); auto c = p(3); auto d = r(3); auto e = s(3); auto f = t(3); cout << a.first << endl; cout << a.second << endl; cout << b.first << endl; cout << b.second << endl; cout << c.first << endl; cout << c.second << endl; cout << d.first << endl; cout << d.second << endl; cout << e.first << endl; cout << e.second << endl; cout << f.first << endl; cout << f.second << endl; return 0; }
プログラムの実行結果を以下に示す。いずれの場合も予想通り正しい動きをした。
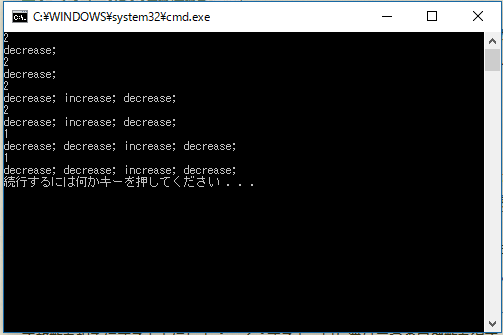
このように純粋な関数と、その合成、および、恒等射としての役割を持つプログラムで構成された圏は、クライスリ(Kleisli)圏と呼ばれる。
また、クライスリ圏はモナド(Monad)と呼ばれるものに含まれる。これについては、また、後の記事で詳しく説明する。
なお、使用された関数のロゴを出力してくるところについてはあまり詳しく説明しなかったが、この部分はモノイド圏になっていることに注意してほしい。
追:\(compose\)については、Milewski氏が圏論の説明をする時に使っていたものをそのまま利用させてもらった。紙面を借りてお礼申し上げる。