ドイツ料理「リンダールーラーデン」を楽しむ

クリスマスが近づくとシュトレン(Stollen)を見かけるようになる。ドイツの菓子パンだが、伝統的にクリスマスの時期に食されている。先日、Kaldiで大量に販売していた。季節ものなので購入したが、少し、甘すぎるかなと感じた。

そうこうするうちに、ドイツ料理には何があるのだろうと考え始めた。市ヶ谷には、パウケというドイツ料理のレストランがある。何回か訪れたことがあるが、本格的な料理を食べた記憶がない。いつも、ビールを飲むことが目的で、ソーセージをおつまみに食べたことしか覚えていない。

インターネットで調べると、グラーシュが出てくる。この料理、以前に記事で紹介した。ドイツのレストランでよく見かける料理ではあるが、ハンガリー起源の料理だ。

さらに検索していくと、ドイツに在住しているご婦人のブログに行きついた。リンダールーラーデン（Rinderrouladen）と呼ばれるドイツの家庭料理を紹介していた。ご主人がドイツ人なので、伝統的な料理なのだろうと思い、少し調べてみた。

ドイツ語で書かれたレシピはたくさんあったが、大体の内容はつかめるものの、正確には読むことができない(大学生の頃には簡単な小説は読めるようになったのに、その後、使う機会がなかったので、すっかり忘れてしまった)。仕方なく、英語のレシピをいくつかさっと読んでみた。

家庭料理ということもあるのだろう。いろいろなレシピがあったが、それらに共通しているのは、薄く切った牛肉に野菜を巻いて長い時間かけて煮込むということであった。

正統な作り方はないようなので、読んだレシピを参考にしながら、リンダールーラーデンなるものを作ってみた。ちなみに、Rinderは「牛肉」を、Rouladenは「巻いた料理」を意味するそうだ。

今日の食材に登場してもらおう。

次に下ごしらえをしよう。玉ねぎ(2個)は、牛肉の中に入れるだけでなく、煮込むためのスープにも用いるので、薄く切る。

さらに、肉に包む分はもう少し小さく切る(1/3程度を細かく。残った場合には煮込み用のスープに入れるので多くても気にしない）。

ピクルス(4本)を細長く切る。

牛肉(350g程度)を広げる。ドイツではリンダールーラーデン用に牛肉を切ってくれるそうだが、日本ではかなわないので、今回は、すき焼き用の肉を購入した。ドイツ料理なので、赤身の方がよいだろうと思い、米国産にした。

さらに、ベーコンを広げた牛肉の上に重ね、マスタードを塗る。

隅の方に、ピクルスと玉ねぎを重ねる。

この上に、塩、コショウ、パプリカをまぶす。

野菜がのっている方から、牛肉を巻く。

料理用のタコ糸で牛肉巻を縛る。

フライパンにバターをひき、牛肉の表面が茶色になる程度まで焼く。


鍋に、残った玉ねぎ、ピクルス、表面を焦がした牛肉をいれ、さらに、赤ワイン(150cc程度)、細かく切ったニンニク(1かけ)、トマトペースト(大匙1杯)、マギーブイヨン(1個)を加える。中火で90分間煮込む。水分が少なくなってきたら、水を少しだけ加える。

リンダールーラーデン(牛肉巻)を取り出す。

鍋に残されたスープを取り出し、煮詰める。
リンダールーラーデンのタコ糸を外し、皿に盛り付け、煮詰めたソースをかけ、食卓に出す。今回は、温野菜とともに食べた。

リンダールーラーデンを真ん中で切断すると、中の野菜が見えてきれいである。

リンダールーラーデンは赤ワインとの相性がよく、おいしくいただいた。ただ、家庭料理にしては、味が強すぎるようにも感じた。マギーブイヨンを入れなくてもよかったような気がした。

称名寺(金沢文庫)を訪れる

称名寺を訪ねた。森茂暁著『闇の歴史、後南朝』を読んだのがきっかけになった。

室町時代の幕開け(1336年)とともに始まった南北朝時代は、1392年に北朝が南朝を吸収して合体することで終了する。その後の歴史は合体を主導した側(北朝)を中心に描かれた。そして、この本が出版されるまでは、南朝のその後について、総括的に記述されることはなかった。合体によって南朝は滅びたと思われがちだが、実はそうではない。そのあと(1479年までの)90年間もの間、室町幕府に反対する勢力のシンボルとなって、幕府の前に立ちはだかっている。このような状況をこの本は詳述している。

この本のなかで、永享(えいきょう)の乱(1438年)についても説明がある。この乱では、将軍権力の拡充を目指す第8代将軍足利義教(よしのり)と将軍職を奪おうとする鎌倉公方足利持氏(もちうじ)が対決した。たいした戦いもなしに、将軍家が勝利する。持氏は称名寺で出家し、その後、永安寺に移され、関東管領上杉憲実(のりざね)を介して義教に赦免を願うが、許されるわけもなく、逆に憲実に攻められ、自害する。

この本で、称名寺が出てくるのはここだけだ。なぜ、1回だけなのに注目したのだろうか。それは、先週の土曜日に横浜歴史博物館で称名寺の古文書を見たことによる。

横浜市あるいはその近辺で義務教育を受けた人は、金沢文庫について学校で説明を受けたことがあると思う。金沢文庫は、鎌倉時代の中期に北条実時(さねとき)が武家の文庫として設置したものである(北条実時は、第2代執権北条義時の孫で、金沢流北条氏の実質初代で金沢実時ともいわれる。これから金沢文庫と呼ばれる)。現在は、神奈川県立金沢文庫になっていて、称名寺所有の資料を保管展示している。今年、これらの資料が国宝となった。

これを記念して、国宝となった称名寺の古文書が横浜市歴史博物館や金沢文庫などで展示されている。先週の土曜日に横浜市歴史博物館で用事があり、そのついでに、称名寺の資料を見学した。

今日(12月16日)は、その続きではないが、称名寺と金沢文庫を訪れた。金沢文庫は撮影禁止であったので、称名寺だけ紹介しよう。

称名寺で最も大きな建物は山門(1818年建立)である。

山門の手前には、塔頭(たっちゅう)光明院表門があった。1665年の建立で、三渓園に移設された建物を別にすれば、造営年代が判明する横浜市内の建物の中では最も古いそうである。
境内の中に入ると、阿字ヶ池がある。

そこには二つの橋がある。
山門よりの橋は、反り橋になっている。

もう一つの橋は平らである。

平らな橋の先には、金堂(1681年建立)がある。

その右側には、釈迦堂(1862年建立)がある。

金沢文庫へはトンネルを抜けるとたどり着く。

称名寺の宗派は真言律宗である。真言宗の開祖は空海(弘法大師)。平安時代始まりの桓武天皇の時世に、最澄(天台宗の開祖)とともに遣唐使で唐にわたった僧だ。真言律宗の開祖はだれなのだろう(ちなみに、律宗の開祖は奈良時代の帰化僧鑑真である)。ウィキペディアで調べてみた。西大寺の興正菩薩叡尊(えいぞん)が中興の祖となっている。

金沢文庫の写真には、忍性菩薩の展示会への案内がある。忍性(にんしょう)は、第5代執権北条時頼の病気平癒のために、金沢文庫創設者である北条実時によって鎌倉に招かれた。時頼の病気回復に成功したのをきっかけに、忍性の師である叡尊を鎌倉に招くこととなった。そのため、実時は、宋版一切経の7,000帖にも及ぶお経全巻を2セット輸入し、1セットを叡尊の西大寺に、もう1セットを称名寺に贈った。

叡尊にあった実時は、叡尊と志を同じにする僧を称名寺に招聘したいと思うようになり、忍性に相談したところ、審海(しんかい)が紹介された。

また、忍性は鎌倉の極楽寺の開山となった。彼は87歳で亡くなったが、多大な功績により「忍性菩薩」と呼ばれることとなった。来年2017年は、忍性生誕800年を迎える。忍性は、貧者や病人の救済に身を尽くしたそうである。特に、ハンセン氏病患者を毎日背負って町に通ったそうである。社会福祉の祖とも言われる。

称名寺は有名なお寺ではあるが、観光客は多くない。今日の見学者は10人前後。散歩に出てきたのであろう、老夫婦が目立った。厳しい寒さの日であったが、快晴だったので、静かなたたずまいを楽しむことができた。また、和泉元彌主演の映画『忍性』の上演も始まったようなので、鑑賞してさらに理解を深めたいと思っている。

国宝・円覚寺舎利殿を初冬に訪れる

何回となく訪れたことがある円覚寺だが、舎利殿だけはいつも遠目に見るだけで、訪れたことがない。今回(12月10日)、運よく、舎利殿を訪れるイベントがあり、それに参加した。

円覚寺は、鎌倉時代の1282年に建立された。モンゴル帝国(元)が日本を攻めてきた元寇、即ち、文永の役(1274年)と弘安の役(1281年)で戦死した両国の武士たちの魂を鎮めるために、第八代執権北条時宗が創建した寺である(モンゴル兵士の鎮魂をも願った時宗の優しい人柄がしのばれる。この他にも国家の鎮護と禅の普及という目的が創建にはあった)。

鎌倉時代の日本の人口は500万人。モンゴルが二回目に攻めてきた弘安の役では、元・高麗軍を主力とした東路軍が約40,000～56,989人、旧南宋軍を主力とした江南軍が約100,000人であったとされている(兵士数はウィキペディアによるが、なぜ、端数があるのだろう。それもとても細かな)。当時の日本の人口の3%にも及ぶ軍隊が押し寄せてきたことになる。現在の人口で換算すると、その数は300万人にも及ぶことになる。想像を超える国難であったが、いわゆる神風、台風が来襲したために、この難を逃れた。

このことによって、我々が学んだ教科書では、時宗はモンゴルの侵略を阻止した英雄として高く評価されていた。しかし、中世の時代の見直しが進むにしたがって、時宗についても評価が分かれている。

元寇が始まる前の1268年には、大蒙古國皇帝奉書をモンゴル皇帝から受け取っている。その内容は次のようになっている。

天の慈しみを受ける大蒙古国皇帝は書を日本国王に奉ず。朕（クビライ・カアン）が思うに、いにしえより小国の君主は国境が相接していれば、通信し親睦を修めるよう努めるものである。まして我が祖宗（チンギス・カン）は明らかな天命を受け、区夏（天下）を悉く領有し、遠方の異国にして我が威を畏れ、徳に懐く者はその数を知らぬ程である。朕が即位した当初、高麗の罪無き民が鋒鏑（戦争）に疲れたので命を発し出兵を止めさせ、高麗の領土を還し老人や子供をその地に帰らせた。高麗の君臣は感謝し敬い来朝した。義は君臣なりというがその歓びは父子のようである。
この事は王（日本国王）の君臣も知っていることだろう。高麗は朕の東藩である。日本は高麗にごく近い。また開国以来時には中国と通交している。だが朕の代に至っていまだ一度も誼みを通じようという使者がない。思うに、王国（日本）はこの事をいまだよく知らないのではないか。ゆえに特使を遣わして国書を持参させ朕の志を布告させる。願わくは、これ以降、通交を通して誼みを結びもって互いに親睦を深めたい。聖人（皇帝）は四海（天下）をもって家となすものである。互いに誼みを通じないというのは一家の理と言えるだろうか。
兵を用いることは誰が好もうか。王は、其の点を考慮されよ。不宣。
至元三年八月 日

古続記(吉田経長の日記)によれば、この国書を受け取った時、朝廷は返書を送ることを提案したが、幕府は黙殺せよと判断したそうである。どちらをとればよかったのかは、この書の読み方によって異なる。

判断の前提に、中国の手紙での「不宣」は対等な関係にあるときに使う結びである、ということを利用できる。これを念頭において、「兵を用いることは誰が好もうか」を解釈すると、圧倒的な兵力で日本を制圧するよりも、穏やかに和平したいと望んでいたのではないかと読める。

さらに、モンゴル皇帝の使者である趙良弼(ちょうりょうひつ)は、1272年に、モンゴル皇帝のクビライに、日本は「占領に値しない」と伝えていた。そのため、クビライは積極的に攻めようと思ってはいなかったのではないかと考えるのが妥当なように思える。

時宗は、漢文で書かれた国書を理解することができず、南宋から来た禅僧の意見を求めたのではないかと予想される。モンゴル帝国に敗れて日本に亡命してきた彼らは、モンゴル帝国と対決するように文章を捻じ曲げて意見を述べたのではないかと想像される。

このような理由から、もし返書を出していれば元寇はなかったのでと考えている学者もいる。

さらに、時宗は、自から戦場に赴こうとすることもなく、また、北条家の名だたる武士を九州に送ることもなく、九州在郷の少弐氏(しょうにし)を大将にするなどして、他人事のように、モンゴルの襲来をかわそうとしている。これは国の命運を握る職にあるものの施策とは思えないということで、時宗の統治者としての能力を疑っている学者もいる。

このように評価の分かれている時宗だが、元寇での犠牲者が多大であったのには、よほどショックだったのであろう。両国の戦死者を鎮魂するために円覚寺を創建した。

円覚寺の開山となったのが無学祖元(むがくそげん)である。彼は、南宋(現在の中国浙江省寧波市)出身の臨済宗の僧である。南宋がモンゴル軍の侵入を受けた後の1279年に、時宗の招きに応じて来日した。彼よりも前に南宋から渡来していた禅僧の蘭溪道隆(らんけいどうりゅう)の死後、彼を引きついで建長寺の住持となり、その後、円覚寺を開山した。

円覚寺にまつわる説明が長くなったが、さて、昨日のイベントの道順に従って、円覚寺を訪れてみよう。

円覚寺は、何度も火災にあっているそうで鎌倉時代からの建物は残っていないそうである。関東大震災(1923年)でも壊滅的な被害を受けたそうで、その時に被害を受けなかった建物はたった二つとのこと(何とも恐ろしい)。そのうちの一つが、三門(山門)である(他の一つは舎利殿がある正続院内の一つの建物)。この門は三つの解脱、空・無相・無願を象徴しているといわれている。江戸時代(1785年)の建物だそうだ。この門を通るときは、「門を通らずに門を通る」ことと、案内をしてくれた副住職の方が仰った。なお、この門は夏目漱石の『門』という小説の舞台になった。『門』の書き出しは次のようになっている。

宗助は先刻から縁側へ坐蒲団を持ち出して、日当りの好さそうな所へ気楽に胡坐をかいて見たが、やがて手に持っている雑誌を放り出すと共に、ごろりと横になった。秋日和と名のつくほどの上天気なので、往来を行く人の下駄の響が、静かな町だけに、朗らかに聞えて来る。肱枕をして軒から上を見上げると、奇麗な空が一面に蒼く澄んでいる。その空が自分の寝ている縁側の、窮屈な寸法に較べて見ると、非常に広大である。

三門の写真は、


また、紅葉も綺麗であった。

副住職の方によれば、今年は11月の初めに寒い時があり、その月の終わりに温かくなったので、早く紅葉になった木と、遅くそのようになった木があるそうで、12月のこの時期に紅葉を楽しめることはあまりないことだそうだ。

次に訪れたのが仏殿である。仏殿は関東大震災で倒壊し1964年に再建された。鉄筋コンクリート造りの建物である。殿内には、円覚寺の本尊である宝冠釈迦如来坐像が安置されている(通常、釈迦如来は頭には何もつけていないが、円覚寺の釈迦如来は宝冠をかぶっているのが特徴である)。

また、天井には前田青邨の監修で日本画家守屋多々志が描いた天井画の「白龍図」がある。

次に説明を受けたのは、選仏場である。ここは僧のための座禅道場である。

この右隣には、居士林があり、一般の人を対象に座禅が行われていた。この日、案内してくれた副住職の方も、民間企業に勤めているときに、この禅道場に通ったそうである。何か思うところがあったのだろう、企業をやめて、修行僧になり、今日に至ったとのこと、彼にとっては今のきっかけとなった場所であると感慨深げに話をしてくれた。

舎利殿に向かう道すがら妙香池を見る。岩が虎の頭に見えるそうだ。その気になれば何となくだが、

さて、今日の目的である舎利殿に入る。舎利殿は神奈川県唯一の国宝建造物である。

舎利殿は、入母屋造で、柿(こけら)葺である(屋根の下部が寄棟造、上部が切妻造のものを入母屋造という)。舎利殿は最初から円覚寺にあったものではないそうだ。尼寺の太平寺の仏殿を移築したもので、室町時代の建物と推察されている。1556年に安房の国の里見義弘が鎌倉を攻めたときに、太平寺も攻撃を受けた。青岳尼と本造聖観音菩薩立像が奪われ、青岳尼は、その後、里見義弘の正室となった。太平寺は廃寺となり、仏殿が円覚寺に移築されたそうだ。

なお、舎利殿は関東大震災で倒壊したが、その写真が文化庁のホームページに掲載されていた。

舎利殿の内部には、仏舎利(釈迦の遺骨)を安置した厨子がある。

舎利殿の周りには、鎌倉でよく見かける「やぐら」があった。

舎利殿の奥の開山堂には、さらに建物があり、無学祖元の像が安置されていた。

また、舎利殿の右横には禅堂があり、修行僧はここで座禅を組むそうである。7日間寝ずに座禅を組む修行も含まれているそうで(午後11時から2時まで横にならずに坐禅の姿勢のままで休む。座睡という)、ゆめゆめ臨済宗の僧侶になりたいと思ってはいけないと感じた。修行僧たちは、ここで、畳一枚での生活をする。座禅を組むときはその半分となる。円覚寺には25人の修行僧がいるとのこと。臨済宗のお寺の中では最大の人数だそうだ。

この後、今日のもう一つの行事を楽しむため大方丈へと向かう。方丈は、大きさを表し、一辺が一丈、即ち、3メートルの正方形である。これが転じて、禅寺での住職の居室あるいは寺の住持を表すようになった。円覚寺の大方丈も、元々は、住職の居場所だったそうだが、禅を広めるために、一般に開放したそうだ。

大方丈の裏には庭園がある。

修行僧の足元にも及ばないのだが、その後、大方丈の横の建物で1時間ほどの座禅をして、帰路に着いた。

初冬にもかかわらず、真っ赤に色づいたもみじに迎えられて、普段見ることができない舎利殿、その内部、さらには、開山堂まで鑑賞することができ、さらには、初めての座禅を体験することができ、有意義な一日であった。

寒くなったらボルシチ

野菜売り場の店頭でビーツを見かけることが多くなった。先日のテレビによれば、昨年に比べて7倍も売り上げが増えたと野菜売り場の担当者が伝えていた。

ビーツは、英語ではbeetrootという。赤蕪とも聞いていたので、カブの一種かと思っていたが、そうではない。ビーツはアカザ科なので、ほうれん草や甜菜の仲間だそうだ。ビタミンや鉄分を多く含むということで、健康野菜として注目され、近年、使う人が増えてきたようである。

ビーツを使った料理と言えば、ボルシチだ。ロシア料理として紹介されることが多いが、本当は、ウクライナの家庭料理である。ソ連邦から分離したウクライナは、クリミア半島の帰属をめぐって、一昨年ロシアと激しく対立したことは、まだ、記憶に新しい。首都はキエフで、世界史の教科書にも出てくる都市だ。一度は訪れてみたいと思っている古都だ。

本格的なボルシチの料理を食べたのは、17年も前のことになる。同僚のロシア人、実は、ウクライナの出身だった彼を蓼科へ招待したことがきっかけである。そのときのお礼にということで、彼の家に招かれた時に、やはりウクライナ出身の奥さんの手料理であるボルシチをご馳走になった。素晴らしい味であったが、それにもまして、鮮やかな赤がとても印象的だった。

ビーツの話をあちらこちらで聞くうちに、色彩が印象に残っていた料理の思い出がよみがえり、一度作ってみたいと思うようになった。本来ならば、彼の奥さんからレシピを聞けばよいのだが、急に思い立ったので、日本語と英語の料理関連のホームページを手繰っての作品となった。本格的とはいかないかもしれないが挑戦した。

シチューを作るのと同じ要領なのだが、ビーツとサワークリームを使うことに特徴がある。以前にビーツを見かけたことのあるお店に出かけたが、残念ながら手に入れることができず、今回は缶詰を用いることにした。

例によって、今回の料理の仲間たちだ。

主役のビーツが缶詰の中に納まっているのは残念だ。ビーツそのものは相当に硬そうな根菜なので、缶詰を用いれば下ごしらえの手間を省ける。最初のステップとしては悪くない選択だ。

最初は、スープの素を作る。カレー用の牛肉(250g)を湯通しして臭みを抜く。

湯通しした熱湯は捨てて、牛肉が残った鍋に水(900cc)とマギーブイヨン(1個)を加えて、15分ほど煮る。

この間十分な時間があるので、野菜の下ごしらえをする。セロリ(1/2本)とキャベツ(1/4個)は1cm幅に切る。トマト(2個)は熱湯をかけて湯むきをした後、ざく切りにする。ジャガイモ(2個)は一口大に切って水に浸しておく。

さらに、玉ねぎ(1個)とニンニク(1片)はみじん切りにする。

別のフライパンを用意して、バター(2個、大さじ2程度)と玉ねぎ、にんにくを加える。

これを、野菜に透明感が出るまで炒めて、赤ワインビネガー(大匙2杯)、砂糖(小匙1杯)、塩(小匙1/2杯)を加えて、ひと煮たてする(ビネガーが嫌いな場合には赤ワインで代用)。

これを、牛肉を15分間煮た鍋に加える。

さらに、キャベツ、セロリ、トマトを加える。

そしてこれを10分ほど煮る。この間、時間があるので、ビーツの下ごしらえをする。
ビーツは缶詰半分ほどを用い、少し太めにせん切りにする。

煮終わったところで、

ビーツとジャガイモ、さらには缶詰のビーツの汁(半分)を鍋に加える。

ジャガイモに味がしみ込んだ方がおいしくなるので、最初は中火でその後弱火にして30分ほど煮込む。

出来上がったボルシチを器に移し、この上にパセリを加え、さらに、サワークリーム(90cc)と生クリーム(50cc)を混ぜたものを適量(大匙1－2杯)加える。

サワークリームの味と、少しコリコリするビーツがまじりあって、おいしくいただけた。

少し残ったので、今朝もいただいた。ビーツの赤とサワークリームの白が混じりあい、ピンク色となったボルシチは見た目にもきれいだ。

今度、機会があれば、同僚のウクライナ出身の奥さんにレシピを伺い、本格的なボルシチに挑戦してみたい。

秋深き伊豆修善寺を訪れる

11月末(27日―30日)に別荘の冬仕度をするために伊豆に出かけた。旅行する3日前(24日木曜日)には、東京では観測史上初の11月の積雪を記録した。我が家の庭もちょっとした風情を感じさせる冬景色になった。

伊豆は暖かいところと思われがちだが、別荘のある地帯は箱根と同じように冬は厳しい。まだ、雪が残っているのではないかと心配して出かけたのだが、案の定、登っていくうちに道端の雪が増えてきて、駐車場の入口は吹き溜まりの雪で封鎖されていた。仕方なく、到着した日は雪かきに精を出すことになってしまった。ベランダにもたくさん残っていたので、記念に写真を撮った。

次の日は伊豆修善寺の虹の郷を訪れた。昨日までライトアップしていたとのこと、まだ十分に楽しめた。日本庭園の近くのもみじは下り７分で、地面も朱色に染まっていて、深まり行く秋の景色を醸しだしていた。

今年は、夏目漱石没後100年で、漱石にちなんだ話をあちらこちらで耳にする。NHKは「夏目の妻」を放映した。漱石の妻は悪妻として知られているが、尾野真千子は、癇癪持ちの漱石に耐えながらも、段々に自己を確立していくチャーミングな女性を演じた。表情がとても豊かで、ほのぼのとした温かみを感じさせてくれ、上手な女優さんだなと感心した。そのドラマの中で、夏目の胃潰瘍が悪くなり、修善寺の旅館で、妻鏡子の手厚い介護のもと療養する場面がある。そのとき滞在した旅館の一部(漱石が滞在していた部屋を含む)が虹の郷に移築されている。里山の佇まいを感じさせ、移築前よりも美しい背景の中に溶け込んでいるのではと想像させられる。

日本庭園にほど近い匠の村はこれかららしく、まだ、緑が多かった。

少し離れたところには、二季咲きの桜があったが、冬が迫っている冷たい空気の中、ただ寂しい。

3日目は、修善寺の温泉街に出かけた。最初に、空海(弘法大師)が平安時代初期(807年)に開基した修禅寺を訪れた。最近の観光地は、外国人か老人で占められているが、ここは後者で溢れていた。

修禅寺の庭園が運よく開園していたので、立ち寄った。

伊豆は源頼朝が流された地のため、各所に源氏ゆかりの遺跡がある。修善寺も例外ではないが、しかし、暗い印象を伝えるものが多い。

二代将軍頼家は北条氏との政争に敗れて修善寺に流され、北条時政により入浴中に殺害された。彼の墓は温泉街の中心部の近くにある。

そのそばには、母の北条政子によって、供養のために建立された指月堂がある。

また、温泉街のはずれの山の麓に頼朝の弟の範頼の墓がある。範頼は義経とともに木曽義仲、平氏の討伐に功績を挙げた武将である。二人とも、朝廷から官位を受けたために頼朝から疑われ追われる身となる。範頼は修善寺に幽閉され、梶原景時に攻められ、自害する。

二人の武将の非業の死を悲しむように修善寺のもみじは鮮やかな朱色であった。

プログラマーのための圏論（上）

『プログラマのための圏論』はこれまでの分をまとめてPDFファイルにしました。参考にしてください。

カレー風味のニョッキ

昨日、近くのカルディで三色ニョッキを手に入れた。ニョッキはジャガイモと小麦粉から作られるイタリア料理だ。そこに、トマトを加えると赤に、ほうれん草だと緑になる。これを利用したのが三色ニョッキだ。

ニョッキの由来をウィキペディアで調べてみると、その語源は、「塊」を意味するゲルマン語系の単語knokkaである。もともとは小麦粉を練って作っていた。アメリカ大陸からジャガイモが持ち込まれた後、これを用いるようになったそうだ。

ニョッキを見るとすいとん(水団)を連想することが多い。すいとんは小麦粉を練って作る。ニョッキもすいとんも元々は同じものであったかもしれない。ウィキペディアによれば、すいとんは室町時代の書物には表れてくるそうだ。これよりも古い歴史を持っているのがそばがき(蕎麦掻き)だ。これは小麦粉の代わりにそばを用いる。同じくウィキペディアによれば、そばがきは鎌倉時代には存在したそうだ。

すいとんもそばがきもあまりいいイメージがない。特に、そばがきには悪い印象がまつわりついている。食糧事情があまりよくなかった戦後の時代に、北海道の親せきから暮れになると半端でない量のそば粉が送られてきた。そばにでもと思って送ってきたのだろうが、そばの打ち方を知らない両親は、そばがきにしてくれた。一日か二日ならばおいしいと思ったのだろうが、何日も続けて食べさせられると、見るのも嫌になった。

すいとんも同じように何もない時に食べさせられた記憶があるので、すいとんもそばがきも出会いたくない料理だ(同じような理由で母は戦時中にこればかり食べさせられたというカボチャが嫌いだった)。

すいとんやそばがきを連想させるニョッキはこれまでは避けていたが、赤や緑の色が醸し出す茶目っ気さがこれまでの抵抗感を和らげてくれ、料理に使うことにした。

ニョッキが主張しすぎると、すいとんやそばがきにまつわる芳しくない思い出が呼び起こされるだろうから、少し強い味にしてみようと考え、カレー風味にすることとした。幸い、中村屋のカレー粉が冷蔵庫にしまってあるので、ちょっと高級なカレー味になるようにということで料理を始めた。

今日の食材の仲間たちは、次のとおりである。中央、左側に控えているのが、今日の主役の三色ニョッキである。そして、右側には脇役のシイタケとベーコンである。残りの連中は種類は多いが全て味付け役だ。

まずは、イタリア料理の定番、ニンニク(2かけ)をオリーブオイル(大匙2杯)で炒める。弱火でニンニクの焼けたにおいが出てくるまで続ける。

その後、ベーコン(100g程度)とシイタケ(2個)、さらに、日本酒(大匙2杯)を加えて、中火にして軽く炒める(本当は白ワインを使いたかったのだが、生憎、持ち合わせていなかった)。

次に、牛乳(200CC)、カレー粉(大匙1杯)、パプリカ、クミンハウダー、塩、コショウ(それぞれ少々)を加えて、中火で煮詰める。

鍋にお湯を沸かし、沸騰したところで、塩(大匙1杯)を加える。そして、三色ニョッキを鍋に入れ、水面に浮かび上がってくるまで煮立てる(大体3分程度)。

ニョッキを網ですくって皿に移す。

カレー風味をニョッキの上に注ぐ。

イタリア料理らしくするために、イタリアンパセリとパルミジャーノを用意する。

これを料理の上にパラパラとふってできあがりだ。

食卓にはこのような感じで登場した。

悪い思い出がよみがえることもなく、おいしくいただけた。

プログラムでの圏の構成を完成させる

４．７　C++プログラムから圏を作成する(続き)

前回の記事で、曜日を進めるプログラムの開発状況を手順を追いながら、説明した。このプログラムは、曜日を進める関数\(increase\)と遅らせる関数\(decrease\)から出発した。最初に作った関数は、値をどこにも記憶しない純粋な関数の集まりであった。

しかし、新たな要求が発生したために、呼ばれた関数をログとして出力することが要求された。最初に最も安易な実現方法を示した。それは、グローバル変数にログを記憶するというものであった。プログラム開発に馴染んでいない初心者が陥りやすいミスの一つだが、プログラムを開発するときに心掛けなければならない参照の局所性を犯している。これは重大な欠陥で、一つの事項の変更がプログラムのあちらこちらの変更に砂がるため、後々のプログラムの改変を困難なものにしてしまう。

上記の問題を改善するために、ログを局所変数化して、それを、関数の引数で引き渡すようにした。プログラムは、随分と改善されたのだが、しかし、引数として渡された変数は、その関数での直接的な関心事ではない。恐らく、プログラムが完成してからしばらくたつと、その変数がなぜ渡されてきたのだろうと疑問に思うことになるだろう。これは、関心の分離というもう一つのプログラム開発に当たって注意しなければならない事項を無視していたために生じた。

そこで、それぞれの関数は、不必要なものは一切有しない純粋な関数にして、関数の合成で、要求仕様の変更に対応した。この時の説明で変だなと思った人も多かったのではないかと思う。数学の力が強い人なのだろうと推察する。二つの関数\(f:a \rightarrow b,g:b \rightarrow c\)があった時、それらの関数の合成は、\(h=g \circ f : a \rightarrow c\)である。

これは、プログラムでは次のようになる。

function<c(a)> h(function<b(a)> f, function<c(b)> g) {}

ところが、関数の合成は次のようになっていた。

function<pair<int, string>(int)> compose(function<pair<int, string>(int)> f, function<pair<int, string>(int)> g)
{
	return [f, g](int x) {
		auto p1 = f(x);
		auto p2 = g(p1.first);
		return make_pair(p2.first, p1.second + p2.second);
	};
}

必要なところだけを切り出すと、\(f: int \rightarrow (Int,String), \ g: int \rightarrow (Int,String) \)となっている。

圏論での約束は、\(f\)のコドメインと\(g\)のドメインが一致していなければならないと謳っている。しかし、\(f\)のコドメインは\((Int,String)\)であるにもかかわらず、\(g\)のドメインは\(Int\)である。一致していない。このようなものを、どのようにして合成するのかという疑問がわく。これは、正しい疑問である。

３）クライスリ圏

数学は、公式に縛られる窮屈な世界だと思っている人も多いと思う。実は、そんなことはない。少し、例外的なものが発生したときは、それを含むように、概念を拡張してあげればよい。それによって、新しい体系の数学を作ることができる。

今回の場合も同じようなものだ。\(g\)のドメインは\(Int\)だ。\(f\)のコドメインには\(Int\)が含まれているので、これを利用して、射を合成できるように規則を拡張したらどうだろうかという発想が生まれる。

例えば、二つの対象\(A,B\)に対して(射\(f\)は元々は\(f: A \rightarrow B\)であったのだが)、何らかの要請で、\(f: A \rightarrow (B, C)\)とする必要が発生した。そこで、圏論での約束を少し緩めて、二つの対象\(A,B\)にして、射\(f: A \rightarrow (B, C)\)を射として認めるようにしたらどうであろうか。

この例で行くと、\(increase\)は、元々、\(Int\)から\(Int\)への関数であった。\(decrease\)も同じである。しかし、ログを作成できるようにという要求に合わせるために、これらは\(Int\)から\((Int, String)\)への関数へと変化した。

曜日を進めるプログラムがどのような圏になるかを直感的に理解してもらうために、まず、図を見てもらおう。

そこで、\(increase\)のドメインを\(Int\)とし、整数(曜日)と文字列の対であるコドメインを\(\mathcal{M}(Int)\)で表すこととしよう。即ち、\(increase:Int \rightarrow \mathcal{M}(Int)\)とする。\(decrease,stay\)についても同様である。

そこで、これらの関数は合成するときは、\(\mathcal{M}(Int)\)を\(Int\)に変換する必要がある。関数の合成にはこの機能を持たせることにしよう。そうすると、\(compose(increase,decrease)\)は、図に示したように、\(increase\)を実行した後で、\(decompose\)を実行し、最後に\(decrease\)を実行すると読むことができるので、これらの、ドメインとコドメインの関係は
\begin{eqnarray}
increase: Int \rightarrow \mathcal{M}(Int) \\
compose: \mathcal{M}(Int) \rightarrow Int \\
decrease: Int \rightarrow \mathcal{M}(Int)
\end{eqnarray}
となり、関数の合成に関する約束(合成される関数のコドメインと合成する関数のドメインは一致する)を守ることができる。

次のstayの関数について考えよう。この関数は恒等射と考えているので、入力された曜日はそのままである。またこれまでに実行してきた関数の列に対しても変化を加えてはいけないので、ここでは関数の名前\("stay"\)を出力するのではなく、空の文字列""を出力する。

圏の形になってきたので、その構成を示そう。
1)　対象：\(Day=\{0,1,2,3,4,5,6\}\)
2)　射：\(increase, decrease\)
3)　ドメイン：\(Day\)、コドメイン：\(\mathcal{M}(Day)\)
4)　恒等射：\(stay\)
5)　合成：\(compose\)
①　結合律：満足
②　単位律：満足

結合律、単位律は、プログラムの内容から満たされていると判断できるが、念のため、正しいかどうか調べてみよう。次のような\(main\)のプログラムを作成して検査してみることにした。
最初の2行は恒等射となっている\(stay\)に関するものである。次の4行は、\(compose\)の実行順序によらないことを示すために、左側から実行する場合とそれとは逆の場合で変化が生じるかを調べるものである。

int main()
{
	auto h = compose(stay, decrease);
	auto k = compose(decrease, stay);
	auto p = compose(decrease, compose(increase, decrease));
	auto r = compose(compose(decrease, increase), decrease);
	auto s = compose(decrease, compose(decrease, compose(increase, decrease)));
	auto t = compose(compose(compose(decrease, decrease), increase), decrease);
	auto a = h(3);
	auto b = k(3);
	auto c = p(3);
	auto d = r(3);
	auto e = s(3);
	auto f = t(3);
	cout << a.first << endl;
	cout << a.second << endl;
	cout << b.first << endl;
	cout << b.second << endl;
	cout << c.first << endl;
	cout << c.second << endl;
	cout << d.first << endl;
	cout << d.second << endl;
	cout << e.first << endl;
	cout << e.second << endl;
	cout << f.first << endl;
	cout << f.second << endl;
	return 0;
}

プログラムの実行結果を以下に示す。いずれの場合も予想通り正しい動きをした。

このように純粋な関数と、その合成、および、恒等射としての役割を持つプログラムで構成された圏は、クライスリ(Kleisli)圏と呼ばれる。

また、クライスリ圏はモナド(Monad)と呼ばれるものに含まれる。これについては、また、後の記事で詳しく説明する。

なお、使用された関数のロゴを出力してくるところについてはあまり詳しく説明しなかったが、この部分はモノイド圏になっていることに注意してほしい。

追：\(compose\)については、Milewski氏が圏論の説明をする時に使っていたものをそのまま利用させてもらった。紙面を借りてお礼申し上げる。

C++のプログラムも圏に変えてしまおう

４．７　C++プログラムから圏を作成する

いろいろな圏を見てきたので、ここでは、プログラマーにとっては大事なプログラムを圏として構成することを考えよう。

１）曜日を進めるプログラム

ここで、作成するプログラムを曜日を進めたり遅らせたりするプログラムだ。曜日は数字で表わし、日曜日は０に、月曜日は１というように、日曜日からの昇順で表わすことにしよう。

プログラムに用いる言語は、多くのプログラマが馴染んでいる命令型言語(Imperative Programming Language)を用いることする。ここではC++を使ってみることにしよう。とても久しぶりだが、新しい発見があるかもしれない。そこで、急遽、パソコンにVisual Stadio Communityをインストールし、C++を使えるようにした。開発中の画面を紹介しよう。

上の画面は、ここで紹介するプログラム開発の最終場面である。左側の大きなウィンドウが編集用の画面で、右下の黒いウィンドウが実行画面である。プログラムを編集した後に、[Build]→[Build Solution]で実行ファイルを作成し、[Debug]→[Start Without Debugging]でプログラムを実行できる。編集機能もしっかりしているので、初めてのVisual Studioであったが、プログラムは簡単に作成することができた。

プログラミングをするときには、必要な機能を定めることから始まる。曜日を進めたり、遅らせたりといっているので、一日だけ曜日を進める関数と遅らせる関数が必要になるだろう。これらは、\(increase\)と\(decrease\)という名前を付けて用意しよう。これらの関数は、曜日\(x\)に1を加え、あるいは１減じてそれを７進数で表せばよいので、以下のようなプログラムとなる。\(main\)には、これらの使用例を記述した。

#include "stdafx.h"
#include <iostream>
#include <string>
using namespace std;

int increase(int x)
{
	return (x + 1) % 7;
}

int decrease(int x)
{
	return (x - 1) % 7;
}

int main()
{
	cout << increase(3) << endl;
	cout << decrease(4) << endl;
	cout << increase(2) << endl;
	return 0;
}

簡単なプログラムなので問題はないだろう。ところで、プログラムを作成していると変更が生じるのは、日常茶飯事である。上記のプログラムを実現した後で、呼ばれた関数名のログを作成するようにと要求されたら、どのように応えたらよいであろうか。

次のようなプログラムで対応する魅力に駆られる人も多いことであろう。グローバル変数として\(log0\)を用意し、それぞれの関数の中で、呼ばれるたびに、自身の名前を\(log0\)に付け加える。プログラムで示すと次のようになる。

#include "stdafx.h"
#include <iostream>
#include <string>
using namespace std;

string log0 = "";

int increase(int x)
{
	log0 += "increase; ";
	return (x + 1) % 7;
}

int decrease(int x)
{
	log0 += "decrease; ";
	return (x - 1) % 7;
}

int main()
{
	cout << increase(3) << endl;
	cout << decrease(4) << endl;
	cout << increase(2) << endl;
	cout << log0 << endl;
	return 0;
}

上記のプログラムは、変更箇所が少ないので、将来の変更を考えない人は、この魅力に惑わされてしまう。しかし、このプログラムは、将来の変更には脆弱である。例えば、\(log0\)という名前がよくないので変更ということになると、全ての関数がその影響を受ける。名前の変更程度ならよいが、最近人気が出てきている並列処理で実行できるようにしたいとなった時、\(log0\)にアクセスしているすべての場所で変更が要求される。

これは、プログラムが参照の局所性(Locality of Reference)を守っていないことによる。そこで、引数で渡すことにして、次のように、プログラムを実現した。

#include "stdafx.h"
#include <iostream>
#include <string>
using namespace std;

pair<int, string> increase(int x, string log0)
{
return make_pair((x + 1) % 7, log0+"increase; ");
}

pair<int, string> decrease(int x, string log0)
{
return make_pair((x - 1) % 7, log0 + "decrease; ");
}

int main()
{
string log0 = "";
auto a = increase(3, log0);
auto b = decrease(4, a.second);
auto c = increase(2, b.second);
cout << a.first << endl;
cout << b.first << endl;
cout << c.first << endl;
cout << c.second << endl;
return 0;
}

かなり見やすくなってはいるのだが、それぞれの関数で\(log0+...\)とあるのが気になる。それぞれの関数で、\(log0\)がなんであるかは知らなくてもよいことのように思われる。関係ないものを分離することを関心の分離(Separation of Concerns)というが、個々の部分はこの原理を犯しているように思われる。

そこで、プログラムをさらに改善することにする。関数\(increase\)と\(decrease\)はそれぞれ、計算の結果と関数の名前を対にして出力するように改める。このようにすれば、それぞれの関数は、その関数に求められている必要最小限のことだけを行い、それ以外のことはしないようにすることができる。

２）圏に移す

これらの関数は次から次へとと呼ばれるが、これは、関数の合成で表すこととしよう。即ち、二つの関数\(f:a\rightarrow b,g:b\rightarrow c\)がこの順番で呼ばれた時、\(h=g \circ f : a \rightarrow c\)となるようにしよう。
プログラムは次のような形になる。

function<c(a)> h(function<b(a)> f, function<c(b)> g) {}

また、この関数の戻り値は、関数の本体である。これはラムダ関数として返すようにする。これに注意して、\(compose\)を実現してみよう。

function<pair<int, string>(int)> compose(function<pair<int, string>(int)> f, function<pair<int, string>(int)> g)
{
	return [f, g](int x) {
		auto p1 = f(x);
		auto p2 = g(p1.first);
		return make_pair(p2.first, p1.second + p2.second);
	};
}

プログラム全体を示すと以下のようになる。

#include "stdafx.h"
#include <iostream>
#include <string>
using namespace std;

pair<int, string> increase(int x)
{
	return make_pair((x + 1) % 7, "increase; ");
}

pair<int, string> decrease(int x)
{
	return make_pair((x - 1) % 7, "decrease; ");
}

function<pair<int, string>(int)> compose(function<pair<int, string>(int)> f, function<pair<int, string>(int)> g)
{
	return [f, g](int x) {
		auto p1 = f(x);
		auto p2 = g(p1.first);
		return make_pair(p2.first, p1.second + p2.second);
	};
}


int main()
{
	auto h = compose(increase, decrease);
	auto p = compose(decrease, compose(increase, decrease));
	auto r = compose(decrease, compose(decrease, compose(increase, decrease)));
	auto a = h(3);
	auto b = p(3);
	auto c = r(3);
	cout << a.first << endl;
	cout << a.second << endl;
	cout << b.first << endl;
	cout << b.second << endl;
	cout << c.first << endl;
	cout << c.second << endl;
	return 0;
}

mainで、関数をいくつか合成し、実験してみた。最初の合成は、
\(increase \circ decrease\)である。この合成関数は\(h\)という名前がつけれらている。値を入力すると実行される。
これに続いて\(decrease \circ increase \circ decrease\)と\(decrease \circ decrease \circ increase \circ decrease\)の合成関数を用意した。これらは\(p,r\)という名前がつけれらている。
実行結果は最初の画面の右下の黒いウィンドウである。

関数の合成がを用意したので、圏とするためには、恒等射が必要である。これは、曜日を進めもしなければ遅らせもしない関数である。\(stay\)という名前にして、もらった曜日をそのまま返すようにしよう。なお、関数名はブランクで返すこととする(恒等射にするためだが、説明は後にする)。即ち、

pair<int, string> stay(int x)
{
	return make_pair(x, "");
}

プログラムの全体を示すと次のようになる。

#include "stdafx.h"
#include <iostream>
#include <string>
using namespace std;

pair<int, string> increase(int x)
{
	return make_pair((x + 1) % 7, "increase; ");
}

pair<int, string> decrease(int x)
{
	return make_pair((x - 1) % 7, "decrease; ");
}

pair<int, string> stay(int x)
{
	return make_pair(x, "");
}

function<pair<int, string>(int)> compose(function<pair<int, string>(int)> f, function<pair<int, string>(int)> g)
{
	return [f, g](int x) {
		auto p1 = f(x);
		auto p2 = g(p1.first);
		return make_pair(p2.first, p1.second + p2.second);
	};
}

int main()
{
	auto h = compose(increase, decrease);
	auto p = compose(decrease, compose(increase, decrease));
	auto r = compose(decrease, compose(decrease, compose(increase, decrease)));
	auto s = compose(stay, compose(decrease, compose(decrease, compose(increase, decrease))));
	auto a = h(3);
	auto b = p(3);
	auto c = r(3);
	auto d = s(3);
	cout << a.first << endl;
	cout << a.second << endl;
	cout << b.first << endl;
	cout << b.second << endl;
	cout << c.first << endl;
	cout << c.second << endl;
	cout << d.first << endl;
	cout << d.second << endl;
	return 0;
}

ここまでできたので、次は、これを圏として構成してみよう。少し、説明が長くなりそうなので、記事を改めることにする。

二項演算子からモノイド圏を作る

前回の記事は、ホモトピー論まで含まれていたので、とても高度な数学的概念が含まれていた。それにもめげず、沢山の人が記事を読んでくださったようで、感謝している。今回は現実の世界に戻して、二項演算子の世界を圏にすることを考えよう。

４．６　二項演算子からの圏

単純な圏から複雑な圏へと話を進めてきたが、対象が一つで、射が複数あるいは無数の圏を考えてみよう。小学校で一番最初に学ぶ数学の概念は加算である。二つの自然数を足し合わせて自然数を得るという考え方を学んだのは、記憶の遠くにある小学校の1年生の頃だ。教育熱心の親に育てられた人であれば、すでに、幼稚園の時に学んでいる可能性もある。頭の中に定着している考え方を圏論という立場から整理しなおしてみよう。

小学校の1年生の時に習った足し算は自然数を相手にしていたが、ここでは、そうではなくて整数を相手にするととにしよう。そうすると、足し算は二つの自然数を得て、足した結果(これも自然数になる)を出力する。Haskellでもそのようになっている。

Prelude> 3 + 4
7

このように二つの計算しようとする数の真ん中に置かれる演算子を二項演算子と呼ばれる。あるいは中置関数とも呼ばれる。しかし、関数を用いるときは、一般的には、関数名を書いた後で、変数を並べるのがふつうである。Haskellはこのように記述することも許されている。例えば、足し算の場合には、次のように書くことができる。

Prelude> (+) 3 4
7

１）加法演算子から圏を作成する

これをそのまま圏論の射にしようとすると、射のドメインは二つの整数の対、コドメインは一つの整数となってしまう。このため、演算子の合成(足し算を繰り返し行うこと)をうまく説明することができない。ドメインとコドメインを同じ対象とするためには、入力する整数の数を一つにする必要がある。これは、足される数を演算子の中に含めることで実現できる。Haskellもこれを用意していて、次のように利用することができる。このように多変数の関数を一変数のそれにすることをカリー化(Currying)という。

Prelude> (+3) 4
7

これは一つの圏をなしているが、図で表すと次のようになる。

構成は次のようになっている。
1)　対象：整数\({\mathbb Z}\)
2)　射：\( (+i) \) ここで\(i \in {\mathbb Z}\)
3)　ドメイン、コドメイン：整数\({\mathbb Z}\)
4)　恒等射：\( (+i) \)
5)　合成：\( (+i) \circ (+j) = (+ (i+j) ) \)
①　結合律：満足
②　単位律：満足

Haskellでの合成の例を示しておこう。

Prelude> (+3) . (+4) $ 2
9

二項演算子を圏で表現することに成功したが、他には、方法がないであろうか。二項演算子を関数の合成とし、足される数と足す数をそれぞれ射にするのはどうであろうか。暗黙の裡に整数を集合として考えていたと思うが、モノの見方を全く変えて、これを射と考える。圏論では、射の方が先に来るので、慣れてくるともっともなのだが、集合と言う枠組みの中で考えていると、なかなかこのような発想は浮かばない。

足される数と足す数をそれぞれ射にすると、対象はどうなるのであろうか。射には、ドメインとコドメインが存在しないといけないが、これはシングルトン(Haskellでは()であらわす）ということにしよう。それでは、このように表した圏を図に描いてみよう。

構成は次のようになっている。
1)　対象：シングルトン
2)　射：\(i \in {\mathbb Z}\)
3)　ドメイン、コドメイン：シングルトン
4)　恒等射：\( 0 \)
5)　合成：\( i \circ j = i+j \)
①　結合律：満足
②　単位律：満足

上の例では、合成を加算と見なしていたが、除算と見なせば引き算が、乗算と見なせば掛け算が定義されたことになる(但し、割り算の結果が整数にならない。そうでなくても、ゼロでの割り算が定義されないばかりでなく、計算の順序にもよるので、即ち、\( (24 / 4 )/ 2 \neq 24 / (4 / 2) \)なので、結合律を満たさず、圏とはならない)。

２）あみだくじから圏を作成する

もう少し、馴染みのある例を挙げてみよう。あみだくじだ。今、3人であみだくじを引くことにする。三本の線を引くことになるが、線の置換は以下の6種類に限られる。

そこで、置換前とその後の位置を行列で表し、これを置換行列と呼ぶことにしよう。そして、それぞれの置換行列には名前を付けることにしよう。このようにすると、6種類の置換は次のように表現できる。

\begin{eqnarray}
p_0 &=&
\begin{pmatrix}
1 & 2 & 3 \\
1 & 2 & 3
\end{pmatrix}
,\ p_1 =
\begin{pmatrix}
1 & 2 & 3 \\
2 & 1 & 3
\end{pmatrix}
,\ p_2 =
\begin{pmatrix}
1 & 2 & 3 \\
3 & 2 & 1
\end{pmatrix}
, \\
p_3 &=&
\begin{pmatrix}
1 & 2 & 3 \\
1 & 3 & 2
\end{pmatrix}
,\ p_4 =
\begin{pmatrix}
1 & 2 & 3 \\
2 & 1 & 2
\end{pmatrix}
,\ p_5 =
\begin{pmatrix}
1 & 2 & 3 \\
3 & 2 & 1
\end{pmatrix}
\end{eqnarray}

また、あみだくじの置換は、次の図のように、接続できるものとしよう。

上の図では、\(p_1\)と\(p_1\)の置換行列を接続して新しい置換行列を作成した。新しい置換行列を\(p_2 \circ p_1\)としよう。

それでは二つの置換行列を合成したものを他にも求めてみよう。どの二つを合成しても、6種類の置換行列のどれかに対応することが分かる。
\begin{eqnarray}
p_0 \circ p_0 &=& p_0, \ p_1 \circ p_0 = p_1, \ p_2 \circ p_0 = p_2, \ p_3 \circ p_0 = p_3, \ p_4 \circ p_0 = p_4, \ p_5 \circ p_0 = p_5, \\
p_0 \circ p_1 &=& p_1, \ p_1 \circ p_1 = p_0, \ p_2 \circ p_1 = p_5, \ p_3 \circ p_1 = p_4, \ p_4 \circ p_1 = p_3, \ p_5 \circ p_1 = p_2, \\
p_0 \circ p_2 &=& p_2, \ p_1 \circ p_2 = p_4, \ p_2 \circ p_2 = p_0, \ p_3 \circ p_2 = p_5, \ p_4 \circ p_2 = p_1, \ p_5 \circ p_2 = p_3, \\
p_0 \circ p_3 &=& p_3, \ p_1 \circ p_3 = p_5, \ p_2 \circ p_3 = p_4, \ p_3 \circ p_3 = p_0, \ p_4 \circ p_3 = p_2, \ p_5 \circ p_3 = p_1, \\
p_0 \circ p_4 &=& p_4, \ p_1 \circ p_4 = p_2, \ p_2 \circ p_4 = p_3, \ p_3 \circ p_4 = p_1, \ p_4 \circ p_4 = p_5, \ p_5 \circ p_4 = p_0, \\
p_0 \circ p_5 &=& p_5, \ p_1 \circ p_5 = p_3, \ p_2 \circ p_5 = p_1, \ p_3 \circ p_5 = p_2, \ p_4 \circ p_5 = p_0, \ p_5 \circ p_5 = p_4
\end{eqnarray}

そこで、置換行列を射にしてあみだくじの圏を構成してみよう。
構成は次のようになっている。
1)　対象：シングルトン
2)　射：置換行列\(p_0,p_1,p_2,p_3,p_4,p_5\)
3)　ドメイン、コドメイン：シングルトン
4)　恒等射：\(p_0\)
5)　合成：置換行列の接続
①　結合律：満足
②　単位律：満足

図で示すと次のようになる。

３）モノイド圏

あみだくじが出てきたので、可換群を想像した人は、群論に詳しい人だと思う。

群論の中で一番単純な群は半群である。半群は次のように定義されている。

集合\(S\)とその上の二項演算子\(\circ : S \times S \rightarrow S\)が与えられた時、組\((S, \circ) \)が結合律を満たす時、これを半群という。

さらに、半群が単位元を有するならば、これをモノイド群という。

モノイド圏は、これまで見たきたように、集合の要素を射に、二項演算子を射の合成に、そして、単位元を恒等射にしたものである。このため、モノイド群から作られたものであるので、モノイド圏という。

モノイド群といわれると複雑そうに見えるが、二項演算子を圏にしたものと考えれば納得いくだろう。

様々な関係から圏を作成してみよう

４．様々な圏の作成

圏に馴染むためにいくつかの例を挙げることにしよう。

４．１　空圏

圏の中でもっとも単純な圏は、対象も射も持たない。このため、恒等射も存在しないことになる。これは空圏(圏0)と呼ばれる。その構成を挙げておこう。
1)　対象：なし
2)　射：なし
3)　ドメイン、コドメイン：なし
4)　恒等射：なし
5)　合成：なし
①　結合律：満足
②　単位律：満足

４．２　終端圏

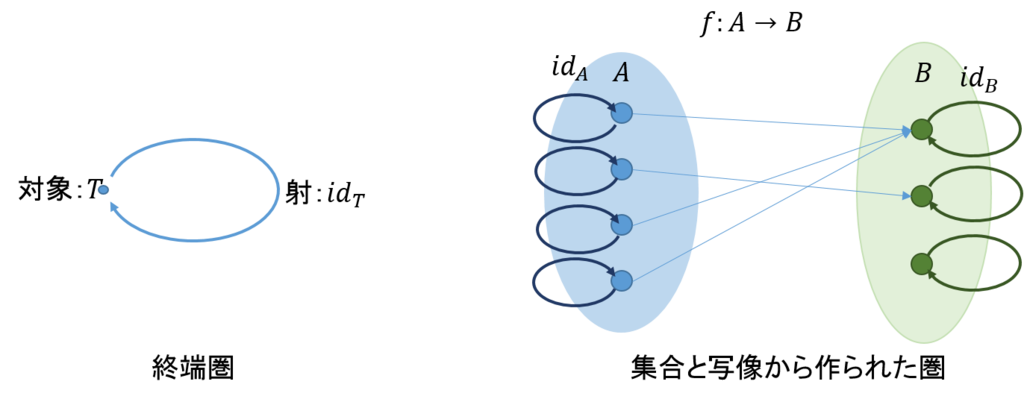
空圏に続いて単純な圏は、対象と射を一つずつ持つ終端圏(自明な圏、圏1)である。これの構成は次のようである。
1)　対象：一つ\(T\)
2)　射：一つ\(id_T\)
3)　ドメイン、コドメイン：\(T\)
4)　恒等射：あり\(id_T\)
5)　合成：\(\circ\)
①　結合律：満足、即ち、\( (id_T \circ id_T) \circ id_T = id_T \circ (id_T \circ id_T) \)
②　単位律：満足、即ち、\(id_T \circ id_T=id_T\)

まだ、関手(functor)の話をしていないが、圏を対象とし、圏から圏への弧を射にすると新たな圏を構成することができる。この圏での始対象となるのが空圏で、終対象となるのが終端圏である。

４．３　二集合と関数からの圏

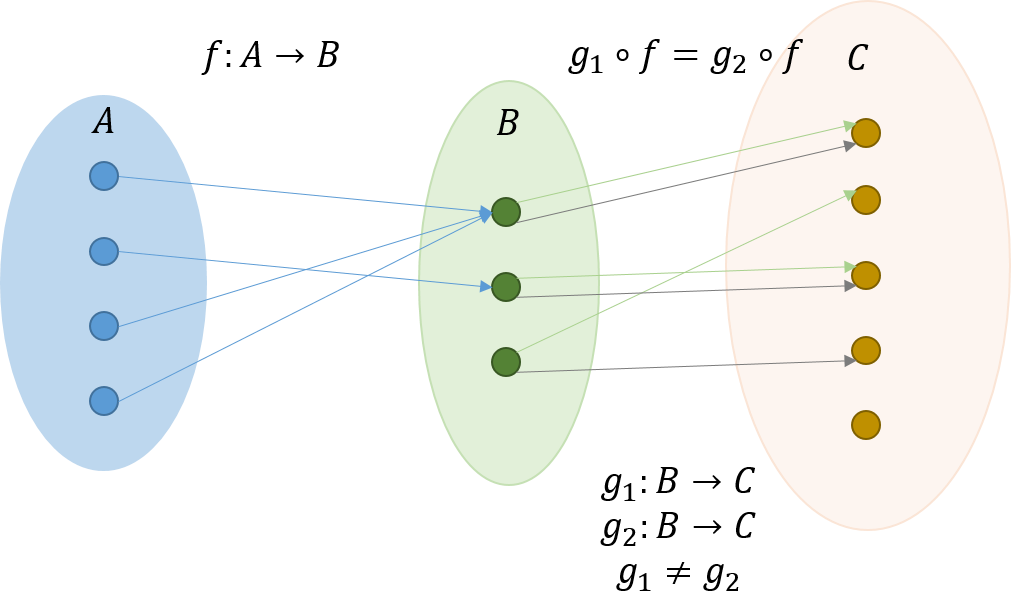
二つの集合\(A,B\)とその間の関数\(f\)は、それぞれの集合に恒等射を用意することで、圏にすることができる。
1)　対象：集合\(A,B\)
2)　射：関数\(f\) 、及び、恒等射と合成された射
3)　ドメイン：\(A\)、コドメイン：\(B\)
4)　恒等射：\(id_A,id_B\)
5)　合成：\(\circ\)
①　結合律：関数が一つなので満足
②　単位律：\(f \circ id_A = f = id_B \circ f\)とする。

図で例を示そう(終端圏の例も同時に示す)。

４．４　グラフからの圏

射が写像だけではなく、関係も表すことができることを説明しよう。最初はグラフである。

グラフには方向のあるものとそうでないものがあるが、ここでは方向のあるものについて扱う。グラフは、節点(node)とそれを結ぶ弧(arc)によって構成される。
グラフからは、次のようにして圏が作成できる。
1)　節点(\(V_1,V_2,V_3,..\))を対象にし、弧(\(f_1,f_2,f_3,..\))を射とする。
2)　さらに二つの連続している弧（片方の弧の終点と他方の弧の始点が同じ節点である）に対しては、これらを接続した弧を新たに作成し、射の中に加える。この操作を、新たな弧が作れなくなるまで繰り返す。
3)　各節点に対して、自身へ向かう弧を作成し、これを恒等射とする。

それでは例で示そう。

1)　左上は与えられたグラフである。
2)　右上は、二つの連続する弧をつなげて加えたものである。
3)　左下は三つの連続した弧をつなげて加えたものである。
4)　右下は恒等射を加えたものである。

出来上がった圏は次のようになっている。
1)　対象：節点\(U,V,W,X,Y,Z\)
2)　射：弧\(f,g,h,k,p,q,r\),及び、恒等射と合成された射
3)　ドメインとコドメイン： \(f:V \rightarrow W, g:W \rightarrow X, h:X \rightarrow Y, k:U \rightarrow Z\), \( p:V \rightarrow X, q:W \rightarrow Y, r:V \rightarrow Y \)
4)　恒等射：\(id_U,id_V,id_W,id_X,id_Y,id_Z\)
5)　合成：\(p=g \circ f, \ q=h \circ g, \ r=h \circ g \circ f =h \circ p =q \circ f \)
①　結合律：\((h \circ g) \circ f = h \circ (g \circ f)\)であるので満足している。
②　単位律：\(f \circ id_V = f = id_W \circ f,...\)であるので満足している。

４．４　順序からの圏

射が関係を表す例の二番手は順序である。順序は、量や質の差によって、順序付けを行うときに使う数学の概念である。順序付けの仕方には強い場合も弱い場合もあるが、その強弱によって、順序には、前順序(preorder)、半順序(partial order)、全順序(total order)の三種類が数学の世界では用意されている。

１）前順序

ATP男子のテニスツアーも一昨日(11月6日)全て終わり、2016年度のシングルスレースの順位が確定した。錦織は、幸い、5位の位置におりロンドンで開催されるATPファイナルに出場できることとなった(上位の8人がファイナルに出場できる。今年は、ナダルが8位だが、怪我のため出場しないので、9位のティエムが繰り上げで参加になった。また、4大オープンに優勝すれば順位に関係なく出場できる)。上位5人の今年度のポイントは次のようになっている。

順位	名前	ポイント
1	マレー	\(11,185\)
2	ジョコビッチ	\(10,780\)
3	ワウリンカ	\(5,115\)
4	ラオニッチ	\(5,050\)
5	錦織	\(4,705\)

ポイントによって、上記のように順位がつけられているけれども、マレーとジョコビッチのどちらが強いかと聞かれた時、戸惑う人が多いのではないだろうか（先週までは、ジョコビッチが1位だった)。二人のこれまでの対戦成績は、29対29と拮抗している。甲乙つけがたい。

しかし、マレーとワウリンカを比べたとき、どちらが強いかと問われた時、マレーだと多くの人が答えるのではないだろうか。対戦成績を比較すると9対7だ。ジョコビッチとはさらにひらいて19対5だ。

だが、ワウリンカは次に続くラオニッチや錦織よりは強そうだ。4大タイトルの試合で2回も優勝している。

このように考えると、上位5人は3グループに分けられそうだ。最強の２人(マレー、ジョコビッチ)、追いかける1人の勇者(ワウリンカ)、次の世代を担う2人(ラオニッチ、錦織)という具合だ。

そこで、この強さの関係を前順序で表すことにしよう。前順序は、マレーとジョコビッチのように、二者間で順序をつけがたい時、即ち、どちらとも言えない時に、用いると便利である。

前順序は、量あるいは質の違いを二項関係\(\leq\)で表し、次の要件が成立することが必要とされる。ここで、\(P\)は集合とし、集合の要素同士を比較しているものとする。
1)　反射律(reflexivity)：任意の\(a \in P\)に対して、\(a \leq a\)である。
2)　推移律(transitivity)：任意の\(a,b,c \in P\)に対して、\(a \leq b\)かつ\(b \leq c\)であれば、\(a \leq c\)である。

\(a \leq b\)を\(a\)は\(b\)よりも強くはないということにしよう(弱いか一緒である)。このように定めると、先の5人のテニス選手の集まりを集合\(P\)とした時、彼らの関係を次図のように表すことができる。

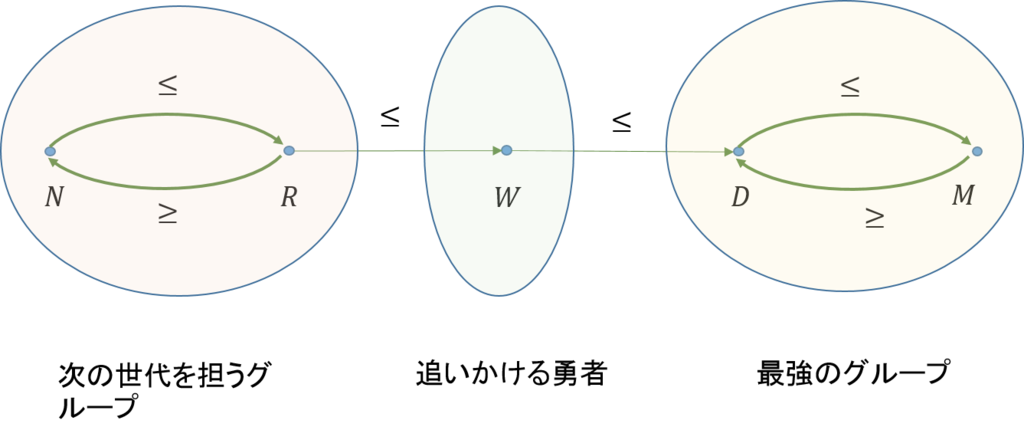
図で節点はテニス選手を表し、それぞれの姓の頭文字で表してある。また、強くはないという二項関係は弧で表してある。また、マレーとジョコビッチのように、強弱がつけがたい場合には、マレーはジョコビッチよりは強くないという関係と、ジョコビッチはマレーよりは強くないという関係の両方を用いて表した。

上の図は、先ほどのグラフと似ていないだろうか。そこで、グラフから圏を求めたときと同じ方法で、この前順序集合を圏に変えてみよう。図に示すような手順で求められる。

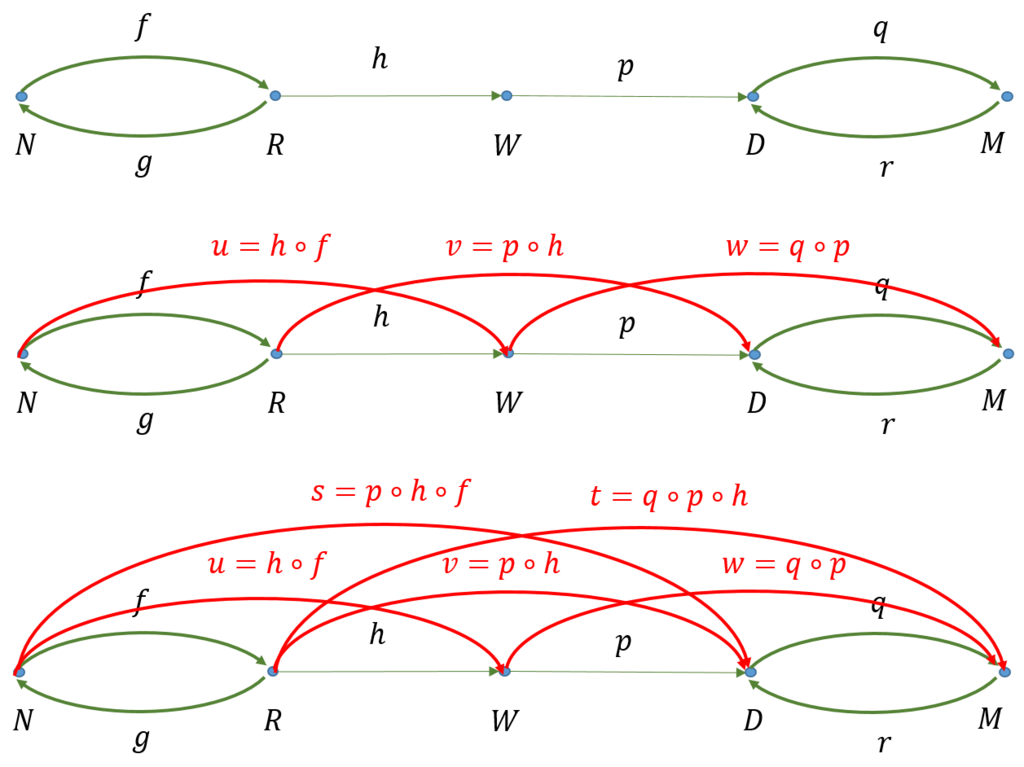
出来上がった圏は次のようになっている。
1)　対象：選手\(N,R,W,D,M\)
2)　射：強弱関係 \(f,g,h,p,q,r,s,t,u,v,w,z\)、及び、恒等射と合成された射
3)　ドメインとコドメイン： \(f:N \rightarrow R, g:R \rightarrow N, h:R \rightarrow W,... \)
4)　恒等射：\(id_N,id_R,id_W,id_D,id_M\)
5)　合成：\(u=h \circ f, \ v=p \circ h, \ w=q \circ p,...\)
①　結合律：\((p \circ h) \circ f = p \circ (h \circ f),...\)であるので満足している。
②　単位律：\(f \circ id_N = f = id_R \circ f,...\)であるので満足している。

２）半順序

位相空間(topological space)を取り上げてみよう。これにはアレルギーがある人も多いことと思う。数学を得意としていた人が、大学に入ってつまずくきっかけとなりやすいのが位相空間だ。ここでは、単に集合と考えてもらっても構わないので、気楽に読んでほしい。

今、全体集合\(X\)と二つの部分集合\(A,B\)が図のように与えられたとしよう。

これから位相空間を作ることにしよう。位相空間を作るためには、開集合あるいは閉集合を用意する必要がある。ここでは、開集合を用意することにしよう。定義は次のようになっている。

位相空間は順序付けられた対\((X,T)\)である。ここで、\(X\)は集合であり、\(T\)は\(X\)の部分集合の集まりで、次の命題を満たす。
1)　空集合\(\{\}\)と\(X\)は\(T\)に属する。
2)　\(T\)のメンバーのいかなる（有限でも無限でもよい）論理和も\(T\)に属する。
3)　\(T\)のメンバーのいかなる有限の数の論理積も\(T\)に属する。

そこで、先に与えられた集合\(X\)と部分集合\(A,B\)から、\(T\)のメンバーを作成してみよう。
与えられた集合と空集合はメンバーに属すので、\(T\)は取り敢えず\(T=\{\{\},X,A,B\}\)となる。そこで、その他のメンバーを探してみよう。

まず、論理和の方から考えると、\(A \cup B\)が得られる。これを\(C=A \cup B\)と名付けよう。他にはなさそうである。メンバーをどのように取ってきてそれらの論理和を取ったとしても、現在のメンバーのどれかになってしまう。そこで、ここまでに得られたメンバーは\(T=\{\{\},X,A,B,C=A \cup B\}\)である。

次に論理積について考えよう。\(A \cap B\)が得られる。これを\(D=A \cap B\)と名付けよう。他にはなさそうである。ここまでに得られたメンバーは\(T=\{\{\},X,A,B,C=A \cup B,D=A \cap B\}\)である。

新たなメンバーが増えたので、もう一度論理和を考える。新しく加わるものはないので、\(T=\{\{\},X,A,B,C,D\}\)となる。

ここで、最初に与えられた集合から位相空間\((X,T)\)を作成することができた。位相空間では、\(T\)のメンバーは集合なので、含むか含まないかの関係を有する。そこで、\(A \leq B\)を\(A\)は\(B\)に含まれるということにすると、\(T\)のメンバーは順序付けすることができる。これは、以下のようなハッセ図となる。

ハッセ図は、半順序集合になっているのだが、半順序をまだ定義していない。そこで、定めておこう。前順序の時と同じように、集合\(P\)の要素同士を比較しているものとする。半順序集合は次の要件を満たすものである。
1)　反射律(reflexivity)：任意の\(a \in P\)に対して、\(a \leq a\)である。
2)　推移律(transitivity)：任意の\(a,b,c \in P\)に対して、\(a \leq b\)かつ\(b \leq c\)であれば、\(a \leq c\)である。
3)　反対称律(asymmetry)：任意の\(a,b \in P\)に対して、\(a \leq b\)かつ\(b \leq a\)であれば、\(a = b\)である。

反対称律は、二つの要素の間には、高々一つの関係しか存在しないことをうたっている。前順序集合では、二つの要素の間に二つの関係が成り立つことを認めていた。テニス選手の例でいえば、錦織とラオニッチの間は甲乙つけがたいということで、\(N \leq R\)と\(R \leq N\)という二つの関係を用意した。

しかし、半順序集合ではこのようなことは許されない。\(N \leq R\)と\(R \leq N\)であれば、\(N = R\)となり、錦織とラオニッチは同じということになる。二人の異なる人間が同じということは何となく気持ちが悪いので、テニス選手の強さを表す時は、半順序ではなく前順序で表した。

前順序では循環(サイクル)が生じることがあるが、半順序では循環が生じない。一方向に進むグラフとなる。それでは、先のハッセ図から圏を求めてみよう。ここでは、答えだけにすると、下図のようになる。

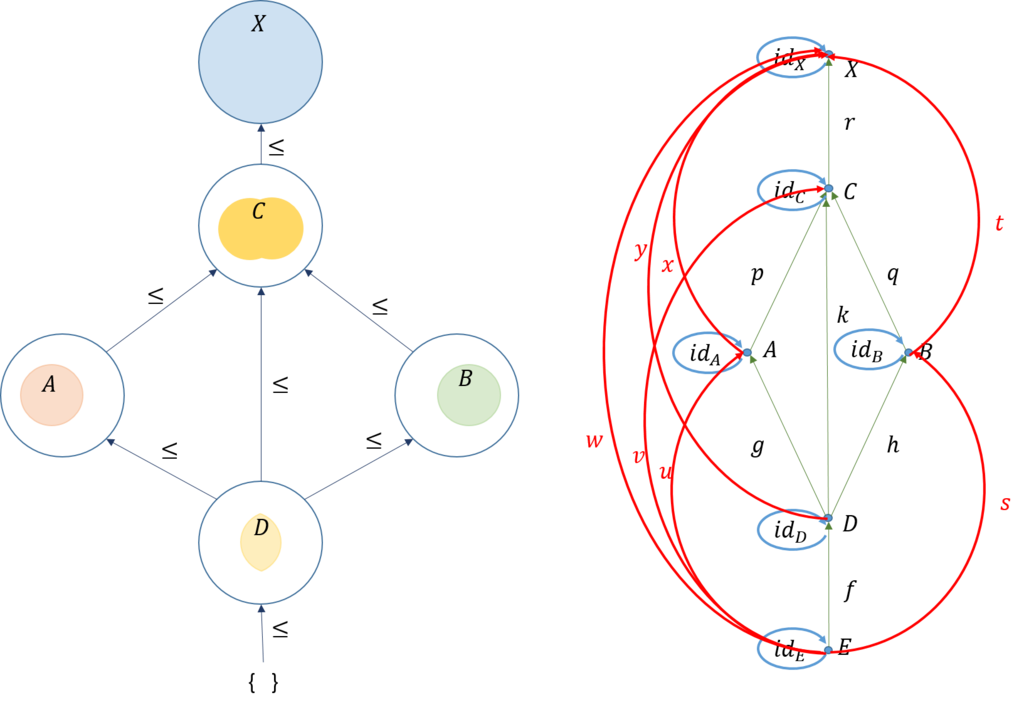
出来上がった圏は次のようになっている。
1)　対象：集合\(X,E,A,B,C,D\)
2)　射：包含関係 \(f,g,h,k,p,q,r,s,t,u,v,w,x,y\),及び、恒等射と合成された射
3)　ドメインとコドメイン： \(f:E \rightarrow D, g:D \rightarrow A, h:D \rightarrow B,... \)
4)　恒等射：\(id_X,id_E,id_A,id_B,id_C,id_D\)
5)　合成：\(u=g \circ f, \ v=p \circ g \circ f, \ w=r \circ p \circ g \circ f,...\)
①　結合律：\((p \circ g) \circ f = p \circ (g \circ f),...\)であるので満足している。
②　単位律：\(f \circ id_E = f = id_D \circ f,...\)であるので満足している。

今、対象\(A\)から\(B\)への写像の集合を\({\rm Hom}(A,B)\)で表すことにしよう。
半順序の場合、任意の二つの接点を結ぶ弧は、最初に説明したように高々一つである。従って、任意の二対象\(A,B\)に対して\({\rm Hom}(A,B)\)の要素の数は高々一つである(空集合かシングルトン)。このように、任意の二対象に対して射の集合の要素の数が高々一つである圏を薄い圏(thin category)という。

薄い圏でかつ循環(サイクル)を有しないとき、全ての射はエピ射であるとともにモノ射である(証明は簡単なので試みること)。集合の世界では、単射で全射である時は、逆関数があることが保証されていた(これを双射(bijective)という)。しかし、循環(サイクル)を有しない薄い圏においては、それぞれの弧はエピ射でありモノ射であるにもかかわらず、逆向きの弧は存在しない（循環することはないため）。即ち、逆射に相当するものは存在しない。このため、エピ射・モノ射と全射・単射は完全に一致する概念ではない。

３）全順序

最後は全順序である。
全順序集合は次の要件を満たすものである。
1)　反射律(reflexivity)：任意の\(a \in P\)に対して、\(a \leq a\)である(この要件は全順序律に含まれるので省いてもよい。ここでは、要件を増やしながら説明しているので、そのまま載せておいた)。
2)　推移律(transitivity)：任意の\(a,b,c \in P\)に対して、\(a \leq b\)かつ\(b \leq c\)であれば、\(a \leq c\)である。
3)　反対称律(asymmetry)：任意の\(a,b \in P\)に対して、\(a \leq b\)かつ\(b \leq a\)であれば、\(a = b\)である。
4)　全順序律(totality)：任意の\(a,b \in P\)に対して、\(a \leq b\)か\(b \leq a\)である。

このように、全ての二つの要素に対して\(\leq\)の関係がつけられるものを全順序と呼ぶ。

建物では、どの二つの階もどちらが高いか比較できるので全順序になっている。二つの階\(A,B\)に対して、\(A \leq B\)を\(A\)は\(B\)よりも高くはないということにすると、図の階\(A,B,C,D\)について、圏を作成すると以下のようになる。

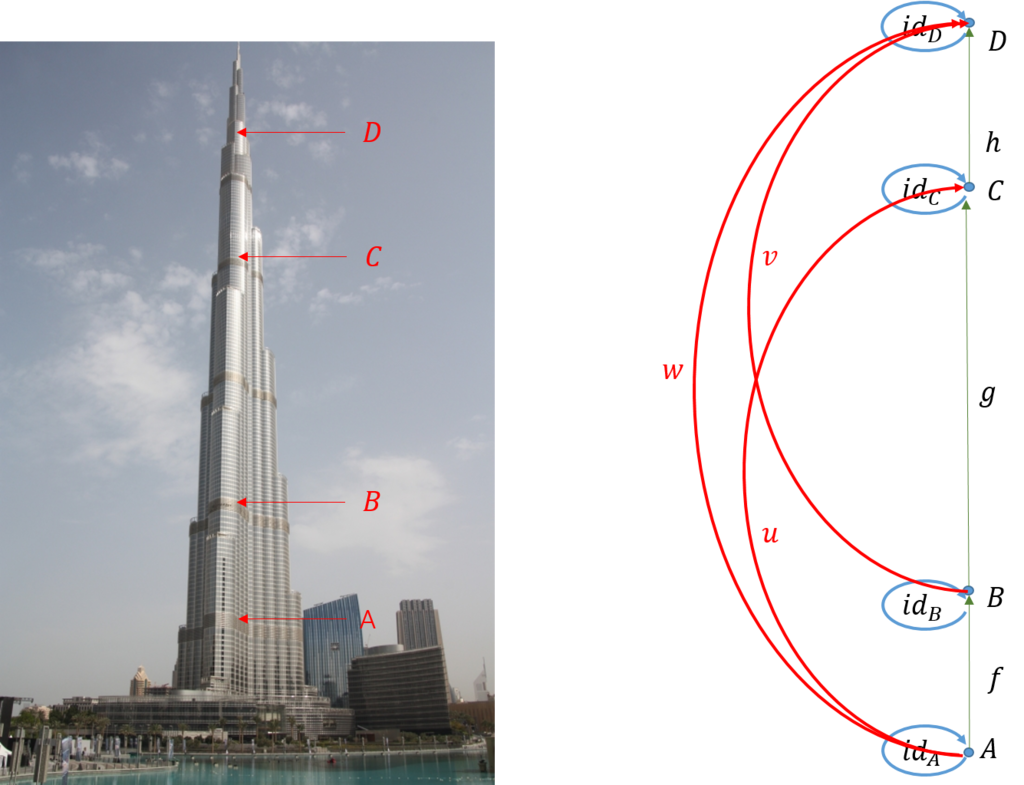
出来上がった圏は次のようになっている。
1)　対象：階\(A,B,C,D\)
2)　射：高低関係 \(f,g,h,u,v,w\),及び、恒等射と合成された射
3)　ドメインとコドメイン： \(f:A \rightarrow B, g:B \rightarrow C, h:C \rightarrow D,... \)
4)　恒等射：\(id_A,id_B,id_C,id_D\)
5)　合成：\(u=g \circ f, \ v=h \circ g, \ w=h \circ g \circ f\)
①　結合律：\((h \circ g) \circ f = h \circ (g \circ f)\)であるので満足している。
②　単位律：\(f \circ id_A = f = id_B \circ f,...\)であるので満足している。

４．５　ホモトピー論からの圏

薄い圏が出てきたので、厚い圏(thick category)の例を挙げよう。二つの対象の間に複数の射があるものが厚い圏になるが、どのようなものがあるだろうか。

位相空間が出てきたので、それより、もっと近代的な数学の一分野であるホモトピー論に登場してもらおう。実は、ホモトピー論とコンピュータ科学の関係は、私事になるが、私の研究分野である。これまでにいくつかの論文を執筆してきた。当初は関心をあまり引かなかったようだが、最近では、少しずつではあるが、読んでくれる人が増えてきて喜んでいる。

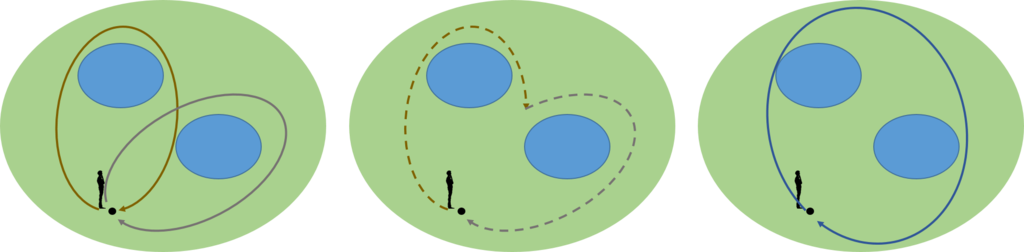
ホモトピー論にまともに立ち向かうと大変なことになるので、その考え方が伝わるように図を多用して説明しよう。下の図は公園である。公園には池が二つある。それらは青色で示してある。

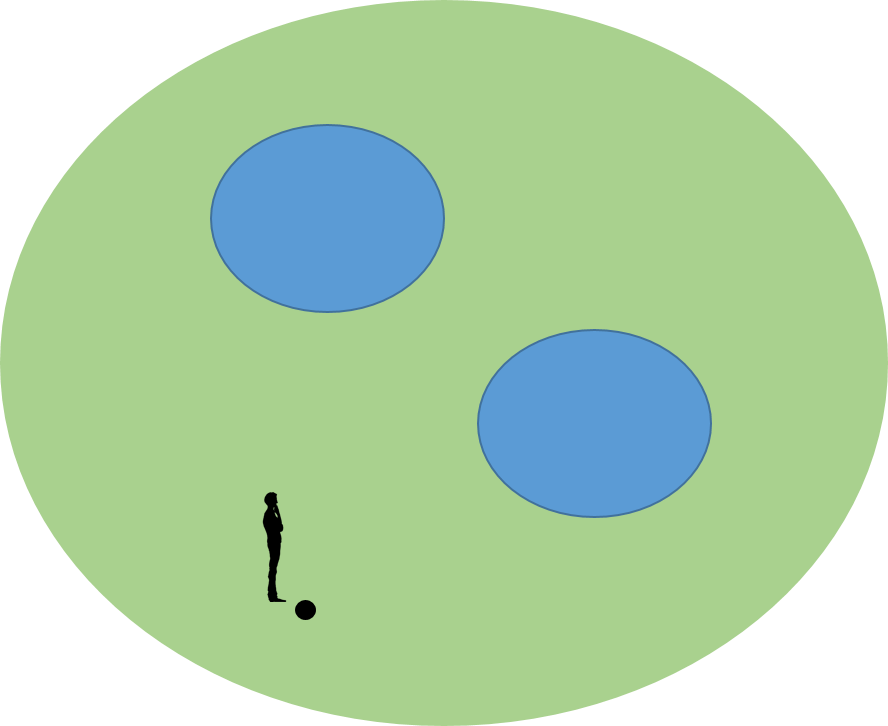
ある人が黒い地点(ここでは基点と呼ぶことにしよう)にいるとしよう。そして、一回りして基点に戻ってくることにする。例えば、池を巡らない方法は、いくつか考えられるが、例えば、図で示したように赤色と黄色の路がある。

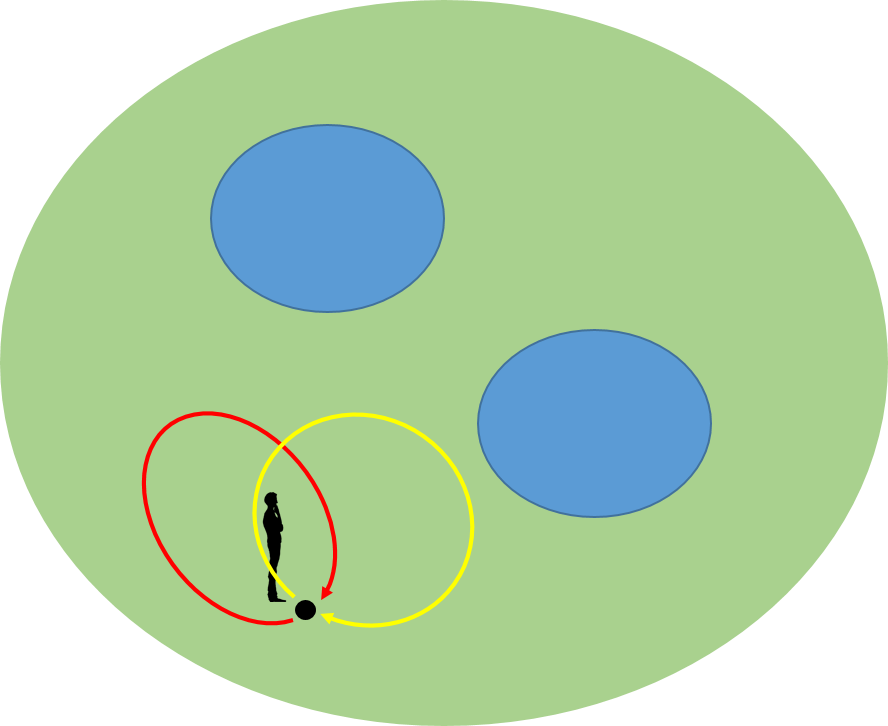
二つの路(Path)は、連続的に変化したときに相手側に行くことができれば、同値な路ということにする。少し工夫すると赤色から黄色の路に連続的に変形して移れることが分かる。

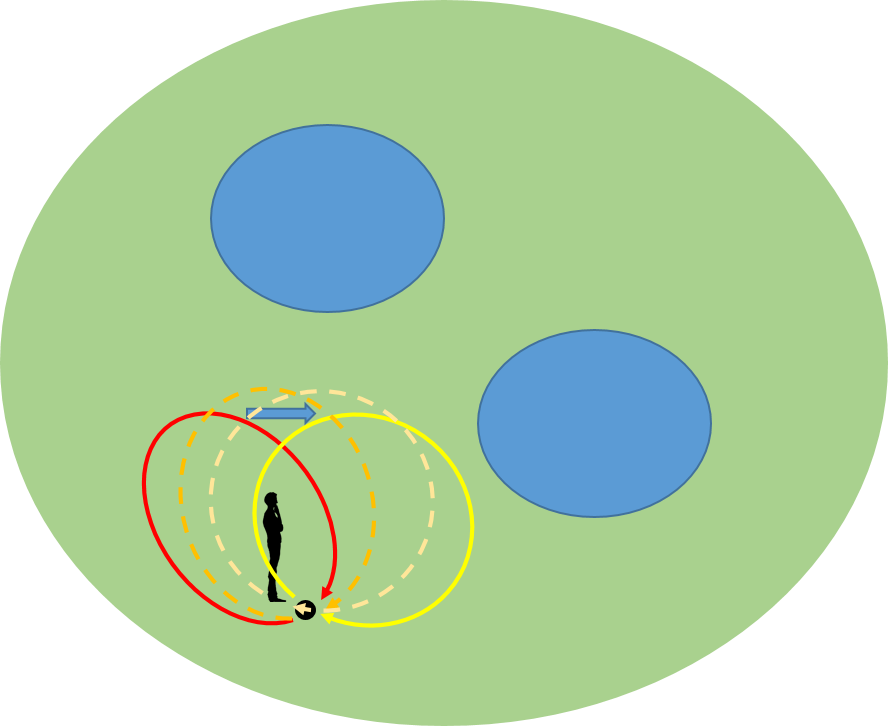
これから、池を巡ってこない路は全て同値ということになる。そこで、池を巡らない路を赤色の路で代表させることにする。

同じように考えると、左側の池を巡ってくる路はすべて同値になる。そこで、池をめぐる路の代表を茶色の路にしよう。

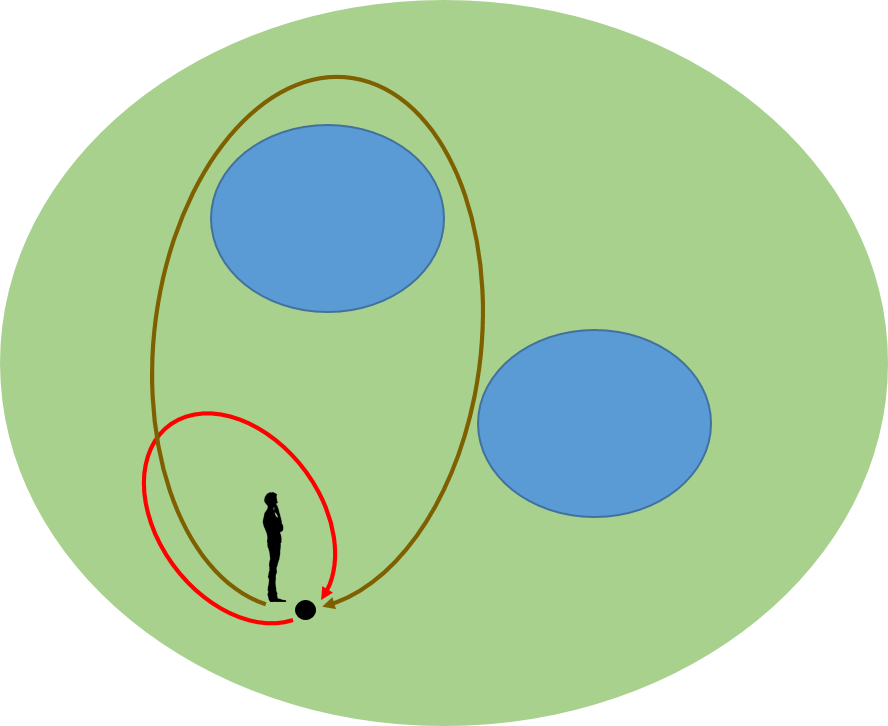
さらに、右の池を巡ってくる路の代表を灰色の路としよう。

これらの路は、お互いに連続な変形をして移ることができないので、独立であるという。この他に独立な路はないであろうか。二つの池をめぐる青色の路はどうであろうか。

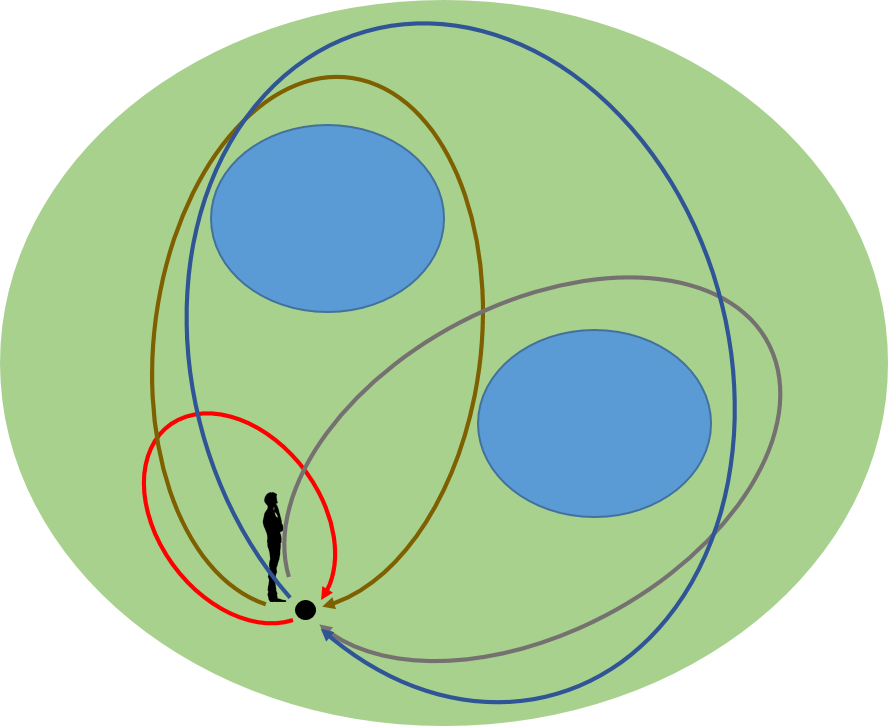
結論から言うと、青色の路は独立ではない。茶色の路を辿った後で灰色の路を辿ることで構成される合成された路を考えてみよう。この合成された路からは、下図に示すように、青色の路に連続的に変形できる路が存在する。従って、青色の路は独立とはならない。

それでは、この公園でのホモトピー的な路を圏にしてみよう。図で示すと次のようになる。

図において、池を巡らない赤色の路は恒等射となる。これは、赤色の路は縮めていくと基点と一致してしまう。これは、基点から動かないことと同じなので、恒等射となる。独立な茶色と灰色の路は、射となる。これらは\(f,g\)で表すことにする。また、赤色の路と灰色の路を何回かたどるのも基点から基点へ至る路であるので、\(f\)と\(g\)を合成したもの(何回用いてもよい)も射である。

1)　対象：基点\(X\)
2)　射：路 \(f, g, s,t,u,.., \)
3)　ドメインとコドメイン： \(X\)
4)　恒等射：池を巡らない路（赤色の路)\(id_X\)
5)　合成：\(\circ\)(基点を軸にして何度も路を回る)
①　結合律：満足している(路の周りかたは、結合の仕方によらない)。
②　単位律：\(f \circ id_X = f = id_X \circ f,g \circ id_X = g = id_X \circ g\)であるので満足している。

路から作られる圏は、無数の射を有していることが分かる。これは、厚い圏の例である。

次の図はトーラスである。

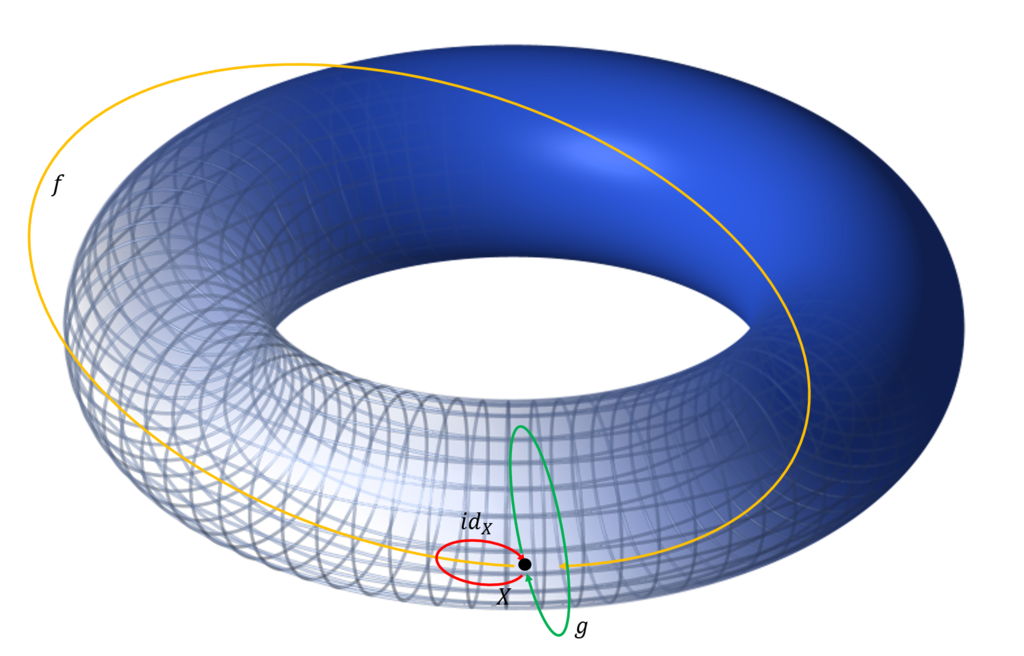
このトーラスと先ほどの公園とは全く違うものに見えるかもしれない。しかし、トーラスの一点を基点とし、そこで、路を考えてみよう。路の一つは、トーラスの穴に沿ってぐるりと回ってくるもの(図では\(f\))である。他の一つは、それとは直角方向にぐるりと回るもの(図では\(g\))である。恒等射となる路は、一周せずに戻ってくるもの(図では\(id_X\))である。他の路はこれらの合成により作られる。従って、トーラスと先ほどの公園は、同じ圏となる。トーラスは３次元で、公園は２次元であるにもかかわらず同じものとみなされる。何とも面白い世界をホモトピー論は扱う。

トーラスだけでなく、下図に示すカップもクラインの壺も同じ圏になる。

ホモトピー論の世界では基本群などを用いて物体の性質を表す。トーラスやクラインの壺の基本群は\({\mathbb Z} \times {\mathbb Z}\)である。\({\mathbb Z}\)は整数を表すが、ここでの意味は、回ってくる回数を表す。

公園の場合には、池の周りをまわる回数となる。逆回りの時は回数を減らすものと考える。従って、回数は、負を含むので、自然数ではなく整数となる。左の池と右の池を回ることは独立であったので、独立な回り方が二通りあるということで、\({\mathbb Z} \times {\mathbb Z}\)と表す。

最近のホットな数学の分野はホモトピー・タイプ論(homotopy type theory)である。この分野でタイプの研究が進むと、Haskellは多大な恩恵を受けるものと期待している。

集合から圏論へ：ミクロな世界からの宇宙への旅立ち（２）

３．２　集合の要素を射に

集合の世界は要素を中心に考えるが、圏論の世界は射を中心に考える。そこで、集合を考えるとき、その要素を射に変えるものが必要となる。
その役割を果たしてくれるのが、一つだけの要素からなる集合である。この集合はシングルトンと呼ばれる。Haskellではデータ型()として用意している。

確認してみよう。まず、()のデータ型を調べるてみよう。

Prelude> :i ()
data () = () 	-- Defined in ‘GHC.Tuple’
instance Bounded () -- Defined in ‘GHC.Enum’
instance Enum () -- Defined in ‘GHC.Enum’

instance Eq () -- Defined in ‘GHC.Classes’
instance Ord () -- Defined in ‘GHC.Classes’
instance Read () -- Defined in ‘GHC.Read’
instance Show () -- Defined in ‘GHC.Show’
instance Monoid () -- Defined in ‘GHC.Base’

ちなみに、\(Int\)と\(Bool\)のデータ型を調べると次のようになっている。

Prelude> :i Int
data Int = GHC.Types.I# GHC.Prim.Int# 	-- Defined in ‘GHC.Types’
instance Bounded Int -- Defined in ‘GHC.Enum’
instance Enum Int -- Defined in ‘GHC.Enum’
instance Eq Int -- Defined in ‘GHC.Classes’
instance Integral Int -- Defined in ‘GHC.Real’
instance Num Int -- Defined in ‘GHC.Num’
instance Ord Int -- Defined in ‘GHC.Classes’
instance Read Int -- Defined in ‘GHC.Read’
instance Real Int -- Defined in ‘GHC.Real’
instance Show Int -- Defined in ‘GHC.Show’
Prelude> :i Bool
data Bool = False | True 	-- Defined in ‘GHC.Types’
instance Bounded Bool -- Defined in ‘GHC.Enum’
instance Enum Bool -- Defined in ‘GHC.Enum’
instance Eq Bool -- Defined in ‘GHC.Classes’
instance Ord Bool -- Defined in ‘GHC.Classes’
instance Read Bool -- Defined in ‘GHC.Read・f
instance Show Bool -- Defined in ‘GHC.Show’

データ型\(Bool\)は\(data \ Bool = False | True\)となっているので、\(False\)と\(True\)二つの要素を取ることが分かる。また、\(Int\)については、その要素はGHC.Typesで定義されていることが分かる。
遡って、シングルトンは、\(Data () = ()\)となっていたので、要素も()であることが分かる。確認してみよう。

Prelude> :t ()
() :: ()

である。::の左側は要素の()で、右側はデータ型の()である。

シングルトンを用いると、集合の要素を射に変えることができる。それは、シングルトンから集合の要素\(a\)へ向かう矢印\(f_a\)を用意することで実現できる。下図は、自然数の集合の各要素を射で表したものである。この場合、射の数は無数になる(但し、数え上げることはできる)。

シングルトンは要素の数が一つだけの集合である。それでは、要素の数がゼロの集合はあるのだろうか。これは、数の議論に似ている。建物で、地面に接している階を、日本では1階にしているが、海外に行くと0階(あるいはGround)となっていることに戸惑った人は多いことだろう。普段の癖で思わず1階のボタンを押してしまい、エレベータのドアーが空いたときそこがロビーでないことにビックリした経験を誰しも持っているのではないだろうか。

数学の世界では、要素の数がゼロの集合が存在する。これは空集合と呼ばれる。前の記事で述べたが、Haskellの世界では\(Void\)として用意している(但し、これを用いるときは、Data.Voidというモジュールをインポートする必要がある)。それでは確認してみよう。

Prelude> import Data.Void
Prelude Data.Void> :i Void
data Void 	-- Defined in ‘Data.Void’
instance [safe] Eq Void -- Defined in ‘Data.Void’
instance [safe] Ord Void -- Defined in ‘Data.Void’
instance [safe] Read Void -- Defined in ‘Data.Void’
instance [safe] Show Void -- Defined in ‘Data.Void’

\(Void\)と呼ばれるデータ型があることが分かる。

\(Void\)は要素が何もないので、真空の状態と見なすことができる。宇宙が真空の状態から埋めれたように、空から有が生じると考えることができる。あるいは、論理の世界では、\(Void\)は偽(\(false\))、シングルトンは真(\(true\))と見なす。論理の世界では、嘘の上にどのようなことを述べたとしても正しいと考えるので、偽からはどのような事でも生みだせると考える（ここでは生み出すものはデータ型）。その役割をしているのが\(absurd\)という関数である。確認してみよう。

Prelude Data.Void> :t absurd
absurd :: Void -> a

\(absurd\)という関数は、任意のデータ型を出力していることが確認できた。\(absurd\)の意味は、常識に反した、理屈に反する、非条理ななどだ。このようなわけで、この関数は用意してあるだけで使うことはまずない。ここでは、それぞれのデータ型はこれから生み出されたと考えておくことにしよう。

要素の数が0と1の集合について話したので、ついでに要素数が2である集合は何であろうか。勿論、偽と真の値を有するブール集合である。Haskellではデータ型\(Bool\)として用意しているが、有用性が高いことは言うまでもない。

集合から圏論へ：ミクロな世界からの宇宙への旅立ち（１）

３．集合の世界から圏論の世界へ

ごちゃごちゃしたミクロの世界をかなぐり捨てて雄大なマクロの世界（宇宙）へ旅立つことにしよう。数学でのミクロな世界は集合で、雄大な宇宙は圏論である。集合は、要素の集まりとして定義される。また、集合を論じるときは、それと一緒に関数(あるいは写像)も学んだことと思う。関数は二つの集合を結びつけるものだ。

圏論では、集合に相当するものを対象(object)と呼び、関数に相当するものを射(morphism)と呼ぶ。集合を論じるときは、ミクロな世界なので、その中に含まれている要素がとても重要な役割をする。しかし、圏論では、マクロな世界を論じるので、対象の中身は気にしないことにする。Haskellでは、対象をタイプとして表すが、常に、タイプを気にし、その構成要素に対してはたいして注意を払わない。

今回の記事では、集合を捨てて対象に、関数を捨てて射に、乗り移れるための準備をしよう（Haskellでは、射を関数と呼んでいるので、少しごちゃごちゃするのだが、Haskellで関数といっているときは、圏論での射と思って欲しい)。

３．１　関数とは

物事を始めるにあたっては、その中で用いる用語の意味をはっきりさせておく必要がある。そこで、ここでは、関数とは何かをはっきりさせておこう。これは、射との違いを考えるうえで助かるはずだ。

少し、基礎的な概念から始めてみよう。プログラムを書くからには、そこに何らかの意思あるいは意図があるはずである。出来上がったプログラムは、そこに、作者の意思あるいは意図を実現しているはずである。そこで、プログラムを書く際に、どのようにして、意思や意味を埋め込んでいくのかが重要になる。

JavaやCのような命令型(imperative)のプログラミング言語を用いれば、意思や意図は、「プログラムのシークエンス(how)」として埋め込まれることになる。HaskellやPrologのような宣言型(declarative)のプログラミング言語を用いれば、それらは「どのようなものであるか(what)」として埋め込まれることになる。

宣言型の説明のところが分かりにくいので、補足しておいた方がよいと思う。プログラムはある特定の領域あるいは特定の問題を対象にして記述される。特定の領域には、それを細かく分解していくと、それ以上は分解できない構成要素(atom)が出てくる。そこで、構成要素の性質あるいは性格をプログラムとして記述する。分解したのとは逆に構成要素を用いて組み立てていくと元の領域に戻るはずである。この作業は構成要素を記述したプログラムの合成で実現する。

例えば、量子力学の世界を考えると、最小の単位は粒子である。これは、数学的にはケットとブラと表すことができる。そこで、ケットとブラを対象(データ型)として表す。ケットとブラに成り立っている関係を射(関数)とその合成で表すことで、量子力学の世界をプログラムで提供できるようになる。

通常、コンピュータ科学の世界では、意思や意図は、意味という。命令型のプログラミング言語を用いて意味を表す方法を操作的意味論(operational semantics)といい、宣言型に対しては表示的意味論(denotational semantics)という。表示的という言葉が使われているのは、構成要素をその特定領域での言葉を用いて表現しているということによる。

１）関係

それでは、表示的意味論での実際的な例を考えることにしよう。代表的なものは、そして、最も多くの場面で使われるのは、関係(relation)だろう。通常の文章でもよく出てくるし、コンピュータの世界でも、データベースでは基本的な概念になっている。例えば、合コンをした時に、望ましいと思った異性をあげることは一つの関係を表している。

ある男性は、一人の女性を望ましいと思ったかもしれない。また、別の男性は、気が多いのか、複数の女性を考えたかもしれない。また、さらに別の男性は、好みがうるさいのか、誰もいなかったというかもしれない。逆に女性側から見たときも、同じようなことが起こる。とても運がよい場合には、二人の好みが合致する場合もある。このような関係を示したのが次の図だ。

数学では、関係は直積集合(Cartesian product)で表される。例えば、次のようになる。男性の方から女性を望ましいと思う関係は、例えば、次のように表される。
\begin{eqnarray}
(Peter, Marry) \\
(Peter, Betty) \\
(Mike, Ellen) \\
(Tom, Michell)
\end{eqnarray}

コンピュータでは、関係は、多くの場合、前述したようにデータベースとして表される。

２）関数

関係は、とても一般的で、二つのグループの関わり合いを形式的に記述するのに都合がよい。しかし、あまりにも自由度が大きすぎるため、数学的な枠組みで使おうとするときは、もう少し、制限の強い概念を用いたほうが都合のよいことが多い。これが関数と呼ばれる。関数は、ドメイン(domain)とコドマイン(codomain)の関係を表すが、そこには、いくつかの約束事がある。
1) 関数には方向性がある。ドメインとコドメインの関係は対等ではなく、矢印がドメインからコドメインの方に向かっている。
2) ドメインの全ての要素に対して、コドマインのある一つの要素が対応する。先ほどの合コンでの例で、好ましい女性がいなかったという男性がいたが、このようなことは許されず、全ての男性は好ましい女性がいなくてはならない。また、複数の女性を好ましいと思う男性がいたがこのようなことも許されない。但し、一人の女性に対して、複数の男性が好ましいと思うこと（多対一対応)は許される。

次の例は、全ての男性が女性一人だけを望ましいといっているので、この関係は関数となる。コドメインの中で、相手のある要素の集まりをイメージという。これらの関係を図で示すと次のようになる。

ドメインの全ての要素に対して相手が割り当てられているような関数を全関数(total function)という。これに対して、ドメインのあるものに対しては相手が割り当てられていないような関数を部分関数(partial function)という。これから扱うすべての関数は全関数である。関数でないものの例を以下に示す。

また、関数の値は変わることがない。このような関数を純粋関数(pure function)という(日本語では純粋関数という用語は使わないようだがここでは便宜的に使う。純粋関数型言語という使い方はあるが、それ以外で使われる例はないようである)。人間の脳は純粋関数ではない。相手に対する好き嫌いは、様々な経験を通して、変化することが往々にしてある。このため、一定であるという保証をすることはできない。一般に、記憶を持つようなものは純粋関数にはならない。

３）逆関数

先ほどは、男性の方から好ましい女性を示す関数\(f\)について説明した。それでは、女性の方から好ましい男性を示す関数\(g\)を考えてみよう。

そこで、関数\(f\)を使って望ましい女性を得た後、関数\(g\)を使ってその女性が、好ましいと思っている男性を求めてみることにしよう。もし、その結果が自身に戻ってくるんであれば、お互いに好ましいと思っているので、こんなに嬉しいことはない。もしすべての男性について、自身に戻ってくるようであれば、男性たちはとても幸せだろう。

逆に、女性の方からも考えてみよう。その場合には、関数\(g\)を施した後で、関数\(f\)を施すことになる。やはり、全ての女性について、自身に戻ってくるようであれば、女性たちはとても幸せだろう。

このようなことが、男性にも、女性にも起こっているとすると、この合コンは理想的な結果をもたらしたといえるだろう。

このことを数学的に記述すると、男性の場合には、
\begin{eqnarray}
g \circ f = id_M
\end{eqnarray}
女性の場合には、
\begin{eqnarray}
f \circ g = id_F
\end{eqnarray}
となる。ここで、\(id_M\)は男性のグループに対する恒等写像、\(id_F\)は女性のグループに対する恒等写像である。

圏論での用語を用いて上記を記述しなおすと、
1) 対象：\(M\)(男性のグループ)、\(F\)(女性のグループ)
2) 射：\(f:M \rightarrow F\)(好ましい女性への射)、\(g:F \rightarrow M\)(好ましい男性への射)
3) 恒等射：\(id_M\)(男性のグループでの恒等射)、\(id_F\)(女性のグループでの恒等射)
4) 合成：\(g \circ f\)、\(f \circ g\)

【圏論の世界での同型写像の定義】
一般に、
\begin{eqnarray}
f:M &\rightarrow & F\\
g:F &\rightarrow & M\\
g \circ f &=& id_M \\
f \circ g &=& id_F
\end{eqnarray}
が成り立つとき、\(f\)と\(g\)は同型写像であるという。数学の概念の中では、重要な概念の一つである。

ここでのポイントは、合成\(\circ\)と恒等射\(id\)を用いて、同型写像が定義されていることである。

上記では、\(M,F,f,g\)について具体的な例を挙げて説明したが、これらはどのようなもので置き換えてもよい。その時、上記のような関係が成り立つとき、\(f\)と\(g\)は同型写像という。また、\(M\)と\(F\)は同型という。

圏論による同型写像の定義の重要性は、対象の要素については何も問うていないことである。細かいことは気にしなくてもよいといっている。また、写像が射に変わっている点である。射は写像を超えるもっと普遍的な概念である。このため、より抽象的な同型を定義するのに役立つ(後々、関手(functor)の話をするがこれは写像をより一般化したものである)。

同型写像は、対象同士が対称(symmetric)であると教えてくれる。あるいは、行って戻れる、すなわち、可逆的(invertible)であるとも知らせてくれる。

同型写像は変化のないモノトーンの世界なのだが、世の中でこのようなことが成り立つことは少ない。同型写像にならない条件は次の通りである。
1) 対象のサイズが異なる。先の合コンの場合、男性と女性の数が異なる場合には、1対1のペアを作ろうとしても、数の多い性の人の誰かが余ってしまう。
2) 多対一対応のものがある。即ち、コドメインのある要素が、二つ以上のドメインの要素から写像される。即ち、\(\exists a, \exists b, a \neq b, f(a) = f(b)\)である。この場合には、二人以上の男性からある女性が望ましいと思われても、その女性は一人の男性しか望ましいと思えないので、破綻してしまうこととなる。

【圏論の世界での逆写像の定義】
関数\(f\)と\(g\)が同型写像である時、\(g\)は\(f\)の逆関数であるという。\(f\)の逆関数は\(f^{-1}\)と書く。同様に、\(f\)は\(g\)の逆関数であるという。

逆関数の例を挙げておこう。今、自然数(0から始まる)と奇数(1から始まる)のグループを考えることにする。自然数のグループの方が奇数のそれよりも2倍だけサイスが大きいと考えがちだが、そんなことはない。

自然数\(x\)から奇数\(y\)への写像\(f\)を\(y=f(x)=2x+1\)とし、奇数から自然数への写像\(g\)を\(x=g(y)=(y-1)/2\)とすると、
\begin{eqnarray}
g \circ f &=& id_\mathbb{ N } \\
f \circ g &=& id_{Odd}
\end{eqnarray}
が成り立つ。

このことから、自然数と奇数は同型であることが分かる。奇数は自然数の部分集合だと思うとなんか変な気分になる。要素の数が無限の時、往々にして、直感が働かない時があるが、これはその例の一つである。

４）全射と単射

圏論の世界から、もう一度、集合の世界に戻ってみよう。この世界では、集合の要素同士がどのように写像されているかが、重要な話題だ。その中から、全射(surjective)と単射(injective)に登場してもらおう。

Surjectiveという単語は、日常会話で用いることはまずないので、初めて見たという人も多いことと思う。この単語は、surとjectiveをつなげたもので、surは、surfaceからも連想できるように、「上」という意味を持つ。語源は古フランス語だ。また、jectは「投げる(の過去分詞)」を意味し、ラテン語を語源としている。

従って、Surjectiveは形容詞「上に投げられた」となる。これに対応した全射という日本語訳もあまり好きではないのだが、関数\(f:A \rightarrow B\)のイメージ\(f(A)\)とコドメイン\(B\)が一致するとき、即ち\(f(A) = B\)のとき、関数\(f\)は全射であるという。

Injectiveは同じようにinとjectiveの合成語である。inは「中へ」という意味だが、この場合には、「そのまま中へ」という意味が含まれているのであろう。別の要素は別の要素へ移すというニュアンスで用いられている。従って、ドメインの任意の二要素\(a,b\)に対して\(a \neq b\)の時、\(f(a) \neq f (b) \)が成り立つならば、関数\(f\)は単射であるという。

単射、全射の例をいくつか示しておこう。

集合の世界では、この二つの用語を用いて、先ほどの同型写像が定義される。

【集合の世界での同型写像の定義】
関数\(f:A \rightarrow B \)が、全射で単射である時、\(f\)は同型写像であるという。

【集合の世界での逆写像の定義】
関数\(f\)が同型写像である時、その矢印の向きを反対にした写像を\(f\)の逆写像という。これを\(f^{-1}\)と記す。

皆さんは、集合の上に定義された同型写像と、圏論の上でのそれとではどちらが好きだろうか。集合の上での定義はアセンブリ言語による定義で、圏論の上での定義は高級言語でのそれに相当すると思うのだが、どうだろうか。

５）エピ射とモノ射

同型写像と逆写像を圏論の世界と集合の世界でそれぞれ定義したので、全射と単射についても圏論の世界で定義してみよう。

まず、全射の方から始める。集合の世界はラテン系の言語を語源としていたので、圏論ではギリシャ系の語源を用いることで、用語も変えてみることとする。ラテン系のチャラチャラした世界からギリシャ系の哲学の世界へ移ろうというと物議を醸しそうだが、気分としてはそんなところだ。surに対応するギリシャ語はepiである。そこで、全射をエピ射(epimorphism)ということにしよう。

また、単射の方は、単一を表すギリシャ語monoを用いてモノ射(monomorophism)ということにする。

それでは、エピ射を定義してみよう。

エピ射でないとすると下図のようなことが発生する。

今、射\(f:A \rightarrow B \)がエピ射でないとする。この時、
\begin{eqnarray}
(g_1 \circ f = g_2 \circ f) \land (g_1 \neq g_2)
\end{eqnarray}
を成り立たせるある対象\(C\)と二つのある射\(g_1: B \rightarrow C\)と\(g_2: B \rightarrow C\)が存在する。
(上の記述を論理式で念のために表しておこう。
\begin{eqnarray}
\exists C,\exists g_1(g_1: B \rightarrow C),\exists g_2(g_2: B \rightarrow C) \\
f(f:A \rightarrow B) \notin Epimorphisms \Rightarrow \\
(g_1 \circ f = g_2 \circ f) \land (g_1 \neq g_2)
\end{eqnarray}
)

そこで、この対偶を取ってみよう。次のようになる（飛躍しすぎだと思う人は、上記の論理式より導き出してほしい）。
全ての対象\(C\)と全ての二つの射\(g_1\)と\(g_2\)に対して
\begin{eqnarray}
(g_1 \circ f \neq g_2 \circ f) \lor (g_1 = g_2)
\end{eqnarray}
の時、射\(f:A \rightarrow B \)はエピ射となる。

そこで、
\begin{eqnarray}
(g_1 \circ f \neq g_2 \circ f) \lor (g_1 = g_2)
\end{eqnarray}
の部分は次のように変えることができる。
\begin{eqnarray}
(g_1 \circ f = g_2 \circ f) \Rightarrow (g_1 = g_2)
\end{eqnarray}
これを利用して次のように定義することができる。

【エピ射の定義】
射\(f:A \rightarrow B \)が次の条件を満たす時、エピ射という。
条件：全ての対象\(C\)と全ての二つの射\(g_1: B \rightarrow C\)と\(g_2: B \rightarrow C\)に対して、
\begin{eqnarray}
g_1 \circ f = g_2 \circ f
\end{eqnarray}
が成り立つとき、
\begin{eqnarray}
g_1 = g_2
\end{eqnarray}
である。[条件終了]

モノ射については、同じように考える。

今、射\(f:A \rightarrow B \)が上図に示すようにモノ射でないとする(上図では異なる矢印のみを記してある。記してない部分は、二つの矢印とも同じ場所から出発して同じ場所にたどり着くので、適当に補って考えること)。この時、
\begin{eqnarray}
(f \circ g_1 = f \circ g_2) \land (g_1 \neq g_2)
\end{eqnarray}
を成り立たせるある対象\(C\)と二つのある射\(g_1: C \rightarrow A\)と\(g_2: C \rightarrow A\)が存在する。

そこで、この対偶を取る。次のようになる。
全ての対象\(C\)と全ての二つの射\(g_1\)と\(g_2\)に対して
\begin{eqnarray}
(f \circ g_1 \neq f \circ g_2) \lor (g_1 = g_2)
\end{eqnarray}
の時、射\(f:A \rightarrow B \)はモノ射となる。

そこで、
\begin{eqnarray}
(f \circ g_1 \neq f \circ g_2) \lor (g_1 = g_2)
\end{eqnarray}
の部分は次のように変えることができる。
\begin{eqnarray}
(f \circ g_1 = f \circ g_2) \Rightarrow (g_1 = g_2)
\end{eqnarray}
これを利用して次のように定義することができる。

【モノ射の定義】
射\(f:A \rightarrow B \)が次の条件を満たす時、モノ射という。
条件：全ての対象\(C\)と全ての二つの射\(g_1: C \rightarrow A\)と\(g_2: C \rightarrow A\)に対して、
\begin{eqnarray}
f \circ g_1 = f \circ g_2
\end{eqnarray}
が成り立つとき、
\begin{eqnarray}
g_1 = g_2
\end{eqnarray}
である。[条件終了]

エピ射、モノ射とも対象の要素を使うことなく、関数の合成だけで定義しているところが大きな特徴である。集合でのそれと比べてどうであろうか。すっきりと見えるのではないだろうか。

追伸

エピ射もモノ射も全ての\(C\),\(g_1\),\(g_2\)に対してといっている。宇宙に存在するものすべてからだと、いつ証明が済むのかなと思ってします。これに代わるものを用意しておいて、この対象とこの射について調べてくれればいいよというものがあると助かる。そこで、これらを用意することにしよう。

モノ射：対象はシングルトンの空間、即ち、\(C=()\)とする。射は、\(A\)の各要素への写像、即ち、\(g_a:() \rightarrow a \in A\)とする。

エピ射：対象は2要素からなる空間、即ち、\(C=\{c_1,c_2\}\)とする。射は、\(B\)を2分し、一方を対象の一つに、他方を対象の残りに写像する、即ち、\(g_{B'}: (B' \subset B \rightarrow c_1 \lor B-B' \rightarrow c_2) \)とする。これの目的は次のようである。対象を2分し、別々の値に写像することで、全ての関数が異なるようになる。なお、\(C\)はブール値の集合\(\{true,false\}\)と考えてもよい。

射は閉じている：どれだけ合成しても大丈夫

２．４　合成

１）圏の構成要素

ここでは、これから説明する合成も含めて、圏を構成する要素についてまとめておこう。圏は次の構成要素から成り立つ。
1)　対象\(A,B,C,..\)を有する。
2)　射\(f,g,h,..\)を有する
3)　射はドメインとコドメインを有する。なお、ドメイン、コドメインは対象である。例えば\(f: A \rightarrow B, g: B \rightarrow C, h: A \rightarrow C,..\)
4)　すべての対象に対して恒等射が存在する。\(1_A: A \rightarrow A, 1_B: B \rightarrow B, 1_C: A \rightarrow C,..\)
5)　コドメインとドメインが一致している射は合成でき、それも射となる。\(f: A \rightarrow B\)で \(g: B \rightarrow C\)ならば、\(g \circ f : A \rightarrow \)が存在する。

なお、圏は次の二つの法則を満たさなければならない。
①　結合律：合成が複数あるとき、結果は、その計算の順序によらず、どれから計算しても同じである。即ち、\( (f \circ g) \circ h = f \circ (g \circ h) \)である。
②　単位律：恒等射とある射の合成は、ある射となる。即ち、\(f \circ 1_A = f = 1_B \circ f\)である。この法則があるため、恒等写像であっても、恒等射とはならないものがある。これについては後で述べる。

２）合成

今回の話題は、圏を構成する要素の中で、合成と呼ばれるものである。合成は、射と射とを結びつけるものである。

射のところで話をしたように、射は、ドメインとコドメインを有する。一つの射のコドメインと他の一つの射のドメインが同じ対象である時、この二つの射は合成できる。

例えば、射\(f:A \rightarrow B,g:B \rightarrow C\)があった時、射\(g \circ f : A \rightarrow C\)が存在する。この時、\( \circ \)を合成という。

いくつか例を挙げよう。

①　対象\(A\)を実数とし、対象\(B\)を整数とし、対象\(C\)を自然数(0から始まる)とし、射\(f:A \rightarrow B\)は小数点以下を四捨五入する関数であるとし、射\(g:B \rightarrow C\)は絶対値をとる関数とする。この時、射\(g \circ f : A \rightarrow C\)は、中心(0)からの整数値による距離(負の値はとらない)を表す。

②　少し変わった合成を定義してみよう。射は自然数(1から始まる)としよう。対象は星とし、すべての射のドメインであり、コドメインであるとする (星なので、対象はあまり意味を持たないと考えてよい)。即ち、任意の自然数\(i\)に対して、\(i : \star \rightarrow \star \) である。

合成は、\(i \circ j : \star \rightarrow \star \)となる。そこで、合成\( \circ \)を乗算とみなしてみよう。即ち、\(i \circ j = i \times j\)とする。この時、合成された射は、これらの射を掛けたものと同じになる。例えば、射3と5の合成は射15と同じである。即ち、\(5 \circ 3 = 15\)である。すべての射は、星自身への射(恒等写像)であるが、単位律を満たすのは1だけなので、これらの射の中で、1だけが恒等射となる。

③　射を0から始まる自然数とし、合成を加算とみなすと、合成された射は、これらの射を加えたものとなる。例えば、射3と5の合成は射8と同じである。上記と同様の理由で、これらの射の中で、0だけが恒等射となる。

④　射を\(+n\),\(n\)は自然数(0から始まる)としよう。また、対象を自然数(0から始まる)とし、すべての射のドメインであり、コドメインであるとする。(図参照)射\(+m\)と\(+n\)の合成は\(+(m+n)\)となる。即ち、\(+m \circ +n = +(m+n)\)である。また、恒等射は\(+0\)である。

⑤　同様に射\(*n\)を考えることができる。この時は、\(n\)は 1から始まる自然数である。この時、恒等射は\(+1\)である。

３）Haskellで実現する。

それでは、Haskellで実現しよう。①から始めよう。0から始まる自然数を必要とするが、これは、前の記事で説明したものを利用する。

data Nat0 = Zero | Succ Nat0 deriving (Read, Eq, Ord, Show)

toNat0 :: Int -> Nat0
toNat0 m
  | m == 0 = Zero
  | m > 0  = Succ $ toNat0 (m - 1)
  | otherwise = error "Not Natural Number"

fromNat0 :: Nat0 -> Int
fromNat0 Zero   = 0
fromNat0 (Succ n) = 1 + fromNat0 n

それでは、四捨五入する関数\(round’\)を定義しよう。Haskellにも\(round\)という関数が用意されているが、この関数は、小数点の数が0.5の時、整数部が偶数のときは切り捨てを、奇数の時は切り上げをする。このため、四捨五入とはなっていないので、次のように定義する。

round' :: Double -> Int
round' m 
  | m >= 0 && m - fromIntegral (floor m) >= 0.5 = 1 + floor m
  | m >= 0 = floor m
  | m - fromIntegral (floor m) > 0.5 = 1 + floor m
  | otherwise = floor m

ここで、\(floor\)は小数点の切り捨てを行う。ただし、負の数の時は、整数部から１引いたものとなる。即ち、\(floor (-4.*)=-5\)である。では、\(round’\)を調べてみよう。

*Main> round' (-3.6)
-4
*Main> round' (-3.5)
-4
*Main> round' 3.6
4
*Main> round' 3.5
4
*Main> round' 3.4
3
*Main> round' 2.6
3
*Main> round' 2.5
3
*Main> round' 2.4
2
*Main> round' (-2.4)
-2
*Main> round' (-2.5)
-3
*Main> round' (-2.6)
-3
*Main> round' (-3.4)
-3
*Main> round' (-3.5)
-4
*Main> round' (-3.6)
-4

それでは、絶対値を求める関数を求めよう。整数を自然数に移すことに注意して、次のようにしよう。

abs' :: Int -> Nat0
abs' m
  | m >= 0 = toNat0 m
  | otherwise = toNat0 (-m)

大丈夫だと思うが、確認してみよう。

*Main> abs' 3
Succ (Succ (Succ Zero))
*Main> abs' 2
Succ (Succ Zero)
*Main> abs' 1
Succ Zero
*Main> abs' 0
Zero
*Main> abs' (-1)
Succ Zero
*Main> abs' (-2)
Succ (Succ Zero)
*Main> abs' (-3)
Succ (Succ (Succ Zero))

それでは、\(round’\)と\(abs’\)の合成関数\(distance\)を次のように定義しよう。

distance = abs' . round'

少し動かしてみよう。

*Main> distance 3.6
Succ (Succ (Succ (Succ Zero)))
*Main> distance 3.5
Succ (Succ (Succ (Succ Zero)))
*Main> distance 3.4
Succ (Succ (Succ Zero))
*Main> distance 2.6
Succ (Succ (Succ Zero))
*Main> distance 2.5
Succ (Succ (Succ Zero))
*Main> distance 2.4
Succ (Succ Zero)
*Main> distance (-2.4)
Succ (Succ Zero)
*Main> distance (-2.5)
Succ (Succ (Succ Zero))
*Main> distance (-2.6)
Succ (Succ (Succ Zero))
*Main> distance (-3.4)
Succ (Succ (Succ Zero))
*Main> distance (-3.5)
Succ (Succ (Succ (Succ Zero)))
*Main> distance (-3.6)
Succ (Succ (Succ (Succ Zero)))

このままだとわかりにくいので、\(fromNat0\)を用いて、整数に変換してみてみよう。

*Main> fromNat0 . distance $ 3.6
4
*Main> fromNat0 . distance $ 3.5
4
*Main> fromNat0 . distance $ 3.4
3
*Main> fromNat0 . distance $ 2.6
3
*Main> fromNat0 . distance $ 2.5
3
*Main> fromNat0 . distance $ 2.4
2
*Main> fromNat0 . distance $ -2.4
2
*Main> fromNat0 . distance $ -2.5
3
*Main> fromNat0 . distance $ -2.6
3
*Main> fromNat0 . distance $ -3.4
3
*Main> fromNat0 . distance $ -3.5
4
*Main> fromNat0 . distance $ -3.6
4

次に、②と③は脇において、④について考えよう。④では、対象を自然数としていたが、ここでは数に変えてみよう(数には整数、有理数、無理数などが含まれる。分かりにくければ、整数と考えてもここでは問題ない)。このように変えると、Haskellで用意している\(+n\)を用いることができる。

(+3)という関数は次のようになっている。さらに、この関数に4を入力する。結果は、4に3くわえられた値7が出力される。

*Main> :t (+3)
(+3) :: Num a => a -> a
*Main> :t (+3) 4
(+3) 4 :: Num a => a
*Main> (+3) 4
7

それでは、合成関数を作ってみよう。+3と+4を合成した関数に、値4を入力してみる。

*Main> (+3) . (+4) $ 4
11

いくつもの関数を合成してみよう。

*Main> (+1) . (+2) . (+3) . (+4) . (+5) $ 4
19

同じことが⑤にも言える。

量子力学とHaskell － 目次

１．身近な存在としての量子力学（１）：MRI（磁気共鳴画像診断装置）、（２）：ヨーロッパコマドリ、（３）：進化論、（４）：光合成、（５）：光合成（続き）、（６）：光合成（続き）、（７）：ケット、（８）：ケットをHaskellで表現する、（９）：重ね合わせ、（１０）：重ね合わせ（続き）、（１１）：ブラ、（１２）：ブラをHaskellで記述する、（１３）：ブラでの重ね合わせをHaskellで表現する、（１４）：重ね合わせの内積
２．量子力学の初歩をHaskellで学ぶ（１）：ブラとケット、（２）：重ね合わせ
３．量子力学の世界を垣間見る（１）：粒子が相互に交換されるモデルの概略、（２）：粒子が相互に交換されるモデル：有限系、（３）：粒子が相互に交換されるモデル：周期系、（４）：ボーズ粒子とフェルミ粒子、（５）：離散系から連続系へ、（６）：ハミルトニアンの活用、（７）：シュレディンガー方程式