前回の記事は、ホモトピー論まで含まれていたので、とても高度な数学的概念が含まれていた。それにもめげず、沢山の人が記事を読んでくださったようで、感謝している。今回は現実の世界に戻して、二項演算子の世界を圏にすることを考えよう。
4.6 二項演算子からの圏
単純な圏から複雑な圏へと話を進めてきたが、対象が一つで、射が複数あるいは無数の圏を考えてみよう。小学校で一番最初に学ぶ数学の概念は加算である。二つの自然数を足し合わせて自然数を得るという考え方を学んだのは、記憶の遠くにある小学校の1年生の頃だ。教育熱心の親に育てられた人であれば、すでに、幼稚園の時に学んでいる可能性もある。頭の中に定着している考え方を圏論という立場から整理しなおしてみよう。
小学校の1年生の時に習った足し算は自然数を相手にしていたが、ここでは、そうではなくて整数を相手にするととにしよう。そうすると、足し算は二つの自然数を得て、足した結果(これも自然数になる)を出力する。Haskellでもそのようになっている。
Prelude> 3 + 4 7
このように二つの計算しようとする数の真ん中に置かれる演算子を二項演算子と呼ばれる。あるいは中置関数とも呼ばれる。しかし、関数を用いるときは、一般的には、関数名を書いた後で、変数を並べるのがふつうである。Haskellはこのように記述することも許されている。例えば、足し算の場合には、次のように書くことができる。
Prelude> (+) 3 4 7
1)加法演算子から圏を作成する
これをそのまま圏論の射にしようとすると、射のドメインは二つの整数の対、コドメインは一つの整数となってしまう。このため、演算子の合成(足し算を繰り返し行うこと)をうまく説明することができない。ドメインとコドメインを同じ対象とするためには、入力する整数の数を一つにする必要がある。これは、足される数を演算子の中に含めることで実現できる。Haskellもこれを用意していて、次のように利用することができる。このように多変数の関数を一変数のそれにすることをカリー化(Currying)という。
Prelude> (+3) 4 7
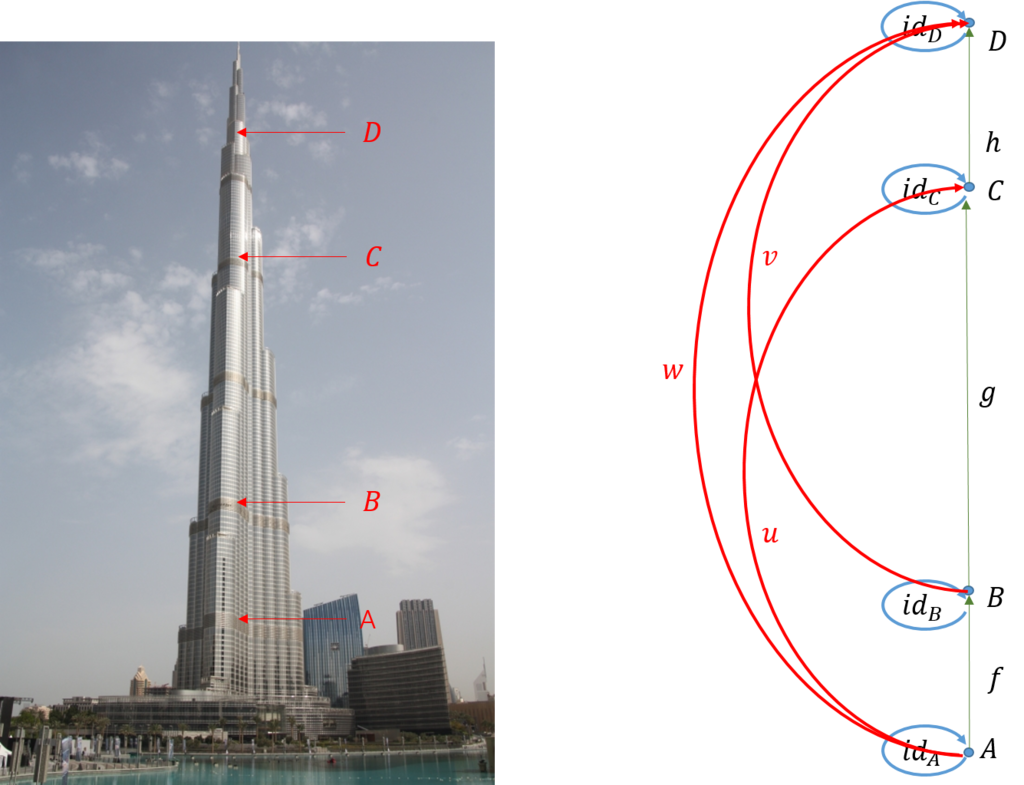
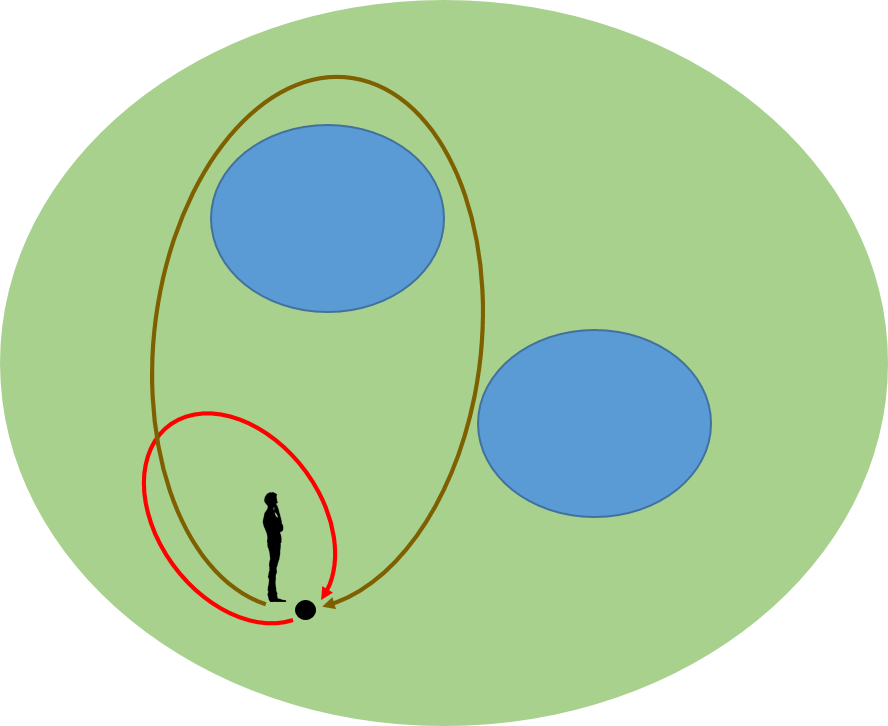
これは一つの圏をなしているが、図で表すと次のようになる。

構成は次のようになっている。
1) 対象:整数\({\mathbb Z}\)
2) 射:\( (+i) \) ここで\(i \in {\mathbb Z}\)
3) ドメイン、コドメイン:整数\({\mathbb Z}\)
4) 恒等射:\( (+i) \)
5) 合成:\( (+i) \circ (+j) = (+ (i+j) ) \)
① 結合律:満足
② 単位律:満足
Haskellでの合成の例を示しておこう。
Prelude> (+3) . (+4) $ 2 9
二項演算子を圏で表現することに成功したが、他には、方法がないであろうか。二項演算子を関数の合成とし、足される数と足す数をそれぞれ射にするのはどうであろうか。暗黙の裡に整数を集合として考えていたと思うが、モノの見方を全く変えて、これを射と考える。圏論では、射の方が先に来るので、慣れてくるともっともなのだが、集合と言う枠組みの中で考えていると、なかなかこのような発想は浮かばない。
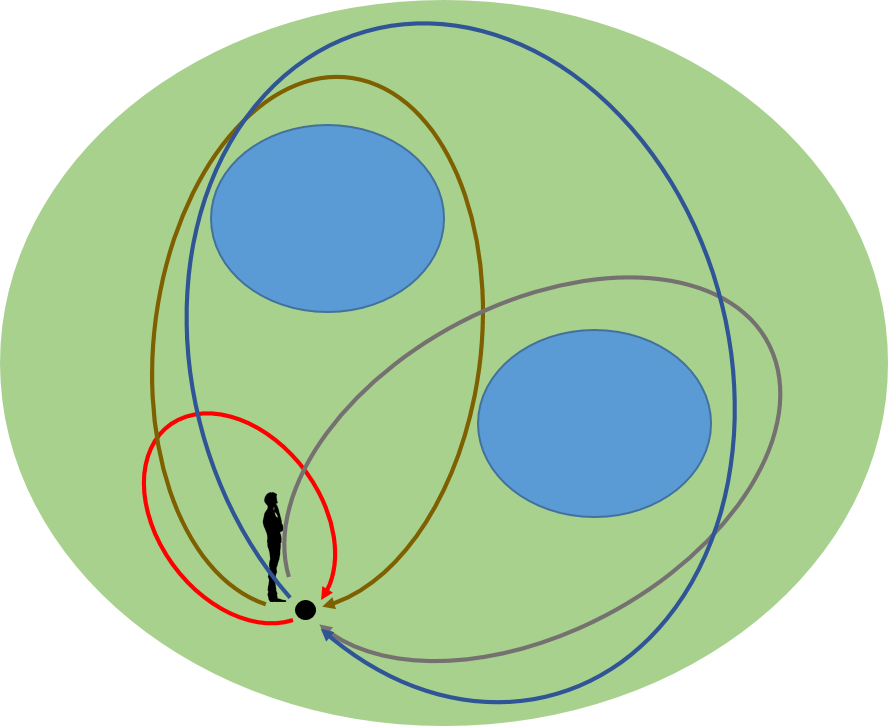
足される数と足す数をそれぞれ射にすると、対象はどうなるのであろうか。射には、ドメインとコドメインが存在しないといけないが、これはシングルトン(Haskellでは()であらわす)ということにしよう。それでは、このように表した圏を図に描いてみよう。

構成は次のようになっている。
1) 対象:シングルトン
2) 射:\(i \in {\mathbb Z}\)
3) ドメイン、コドメイン:シングルトン
4) 恒等射:\( 0 \)
5) 合成:\( i \circ j = i+j \)
① 結合律:満足
② 単位律:満足
上の例では、合成を加算と見なしていたが、除算と見なせば引き算が、乗算と見なせば掛け算が定義されたことになる(但し、割り算の結果が整数にならない。そうでなくても、ゼロでの割り算が定義されないばかりでなく、計算の順序にもよるので、即ち、\( (24 / 4 )/ 2 \neq 24 / (4 / 2) \)なので、結合律を満たさず、圏とはならない)。
2)あみだくじから圏を作成する
もう少し、馴染みのある例を挙げてみよう。あみだくじだ。今、3人であみだくじを引くことにする。三本の線を引くことになるが、線の置換は以下の6種類に限られる。

そこで、置換前とその後の位置を行列で表し、これを置換行列と呼ぶことにしよう。そして、それぞれの置換行列には名前を付けることにしよう。このようにすると、6種類の置換は次のように表現できる。
\begin{eqnarray}
p_0 &=&
\begin{pmatrix}
1 & 2 & 3 \\
1 & 2 & 3
\end{pmatrix}
,\ p_1 =
\begin{pmatrix}
1 & 2 & 3 \\
2 & 1 & 3
\end{pmatrix}
,\ p_2 =
\begin{pmatrix}
1 & 2 & 3 \\
3 & 2 & 1
\end{pmatrix}
, \\
p_3 &=&
\begin{pmatrix}
1 & 2 & 3 \\
1 & 3 & 2
\end{pmatrix}
,\ p_4 =
\begin{pmatrix}
1 & 2 & 3 \\
2 & 1 & 2
\end{pmatrix}
,\ p_5 =
\begin{pmatrix}
1 & 2 & 3 \\
3 & 2 & 1
\end{pmatrix}
\end{eqnarray}
また、あみだくじの置換は、次の図のように、接続できるものとしよう。

上の図では、\(p_1\)と\(p_1\)の置換行列を接続して新しい置換行列を作成した。新しい置換行列を\(p_2 \circ p_1\)としよう。
それでは二つの置換行列を合成したものを他にも求めてみよう。どの二つを合成しても、6種類の置換行列のどれかに対応することが分かる。
\begin{eqnarray}
p_0 \circ p_0 &=& p_0, \ p_1 \circ p_0 = p_1, \ p_2 \circ p_0 = p_2, \ p_3 \circ p_0 = p_3, \ p_4 \circ p_0 = p_4, \ p_5 \circ p_0 = p_5, \\
p_0 \circ p_1 &=& p_1, \ p_1 \circ p_1 = p_0, \ p_2 \circ p_1 = p_5, \ p_3 \circ p_1 = p_4, \ p_4 \circ p_1 = p_3, \ p_5 \circ p_1 = p_2, \\
p_0 \circ p_2 &=& p_2, \ p_1 \circ p_2 = p_4, \ p_2 \circ p_2 = p_0, \ p_3 \circ p_2 = p_5, \ p_4 \circ p_2 = p_1, \ p_5 \circ p_2 = p_3, \\
p_0 \circ p_3 &=& p_3, \ p_1 \circ p_3 = p_5, \ p_2 \circ p_3 = p_4, \ p_3 \circ p_3 = p_0, \ p_4 \circ p_3 = p_2, \ p_5 \circ p_3 = p_1, \\
p_0 \circ p_4 &=& p_4, \ p_1 \circ p_4 = p_2, \ p_2 \circ p_4 = p_3, \ p_3 \circ p_4 = p_1, \ p_4 \circ p_4 = p_5, \ p_5 \circ p_4 = p_0, \\
p_0 \circ p_5 &=& p_5, \ p_1 \circ p_5 = p_3, \ p_2 \circ p_5 = p_1, \ p_3 \circ p_5 = p_2, \ p_4 \circ p_5 = p_0, \ p_5 \circ p_5 = p_4
\end{eqnarray}
そこで、置換行列を射にしてあみだくじの圏を構成してみよう。
構成は次のようになっている。
1) 対象:シングルトン
2) 射:置換行列\(p_0,p_1,p_2,p_3,p_4,p_5\)
3) ドメイン、コドメイン:シングルトン
4) 恒等射:\(p_0\)
5) 合成:置換行列の接続
① 結合律:満足
② 単位律:満足
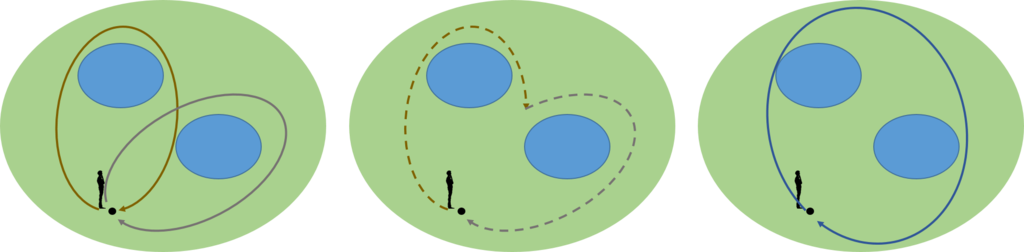
図で示すと次のようになる。

3)モノイド圏
あみだくじが出てきたので、可換群を想像した人は、群論に詳しい人だと思う。
群論の中で一番単純な群は半群である。半群は次のように定義されている。
集合\(S\)とその上の二項演算子\(\circ : S \times S \rightarrow S\)が与えられた時、組\((S, \circ) \)が結合律を満たす時、これを半群という。
さらに、半群が単位元を有するならば、これをモノイド群という。
モノイド圏は、これまで見たきたように、集合の要素を射に、二項演算子を射の合成に、そして、単位元を恒等射にしたものである。このため、モノイド群から作られたものであるので、モノイド圏という。
モノイド群といわれると複雑そうに見えるが、二項演算子を圏にしたものと考えれば納得いくだろう。