2.イベント
関数型リアクティブプログラミングは、シミュレーションに応用すると面白いと思う。そんなことを考えながら、最近、山室京子著『大江戸商い白書』を読んでいる。この本は、江戸時代の商人たちの実像を、当時のデータから数値解析で、明らかにしてくれる。19世紀半ばの江戸の町人人口は27万人である。そのうちの半分近くが、日本橋に集中して居住している。一極集中もよいところだ。町人地区の人口密度は、日本橋ではなんと10坪(33平方米)に4.2人と超過密である。深川あたりでは0.7人となる。家の大きさは、平均すると25.8坪である。
この本には、挿絵がないので、江戸時代の雰囲気を視覚的に把握することができない。別の資料で求めてみると、江東区文化コミュニティー財団が深川江戸資料館で、江戸時代の深川の町を復元している。ホームページにも載っているが、これを使わせてもらうと江戸時代の町人たちの町の様子がもう少しよく分かる。
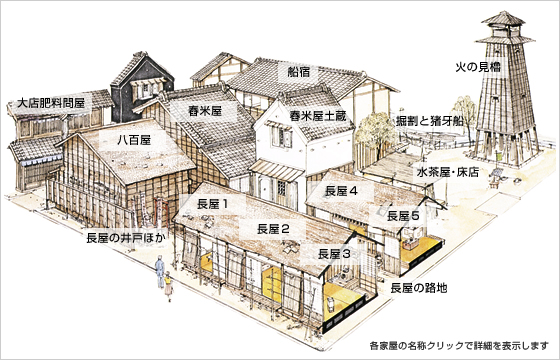
江戸時代の商人たちの動静を知るために、山室が用いたのは、田中康夫編『江戸商家・商人名データ総覧』である。このデータから、よそゆきの江戸とふだんぎの江戸に二分木する(他にも武士を相手にするタイプが存在するが、これを取り除くと二つに分かれる)。よそゆきの江戸で活躍する店(都市型)は、日本橋に集中している呉服屋や薬屋などである(熈代勝覧を見るとその様子が分かる)。ふだんぎの江戸で一生懸命に働く店(全域型)はそこら中に点在する米屋や炭屋などである(精米して小売利する店は舂(つき)米屋と呼ばれた。深川の復元図にも表れている)。二つに分かれた原因を四つの商品特性(消費量、重量、付加価値、多様性)で謎解きしているが、詳しくは、大江戸商い白書を参照して欲しい。
この本の中で、ふだんぎの江戸の市場が、完全競争市場になっていたというくだりが最も面白い。バタバタと倒産して去っていく人がたくさんいる一方で、どんどんと成功を夢見て参入してくる人が多い市場である。参入障壁は小さいが、儲かることは少なく、常に倒産の危機にされされている市場だ。但し、市場は、薄利寡売、生きていくのにやっとの程度しか売れない。米屋だと8.1年、炭屋は12.9年の平均存続年数である。何代にもわたって商売が続くことはなく、ほとんどの場合が譲渡によって他人の手に渡る、厳しい商売である。
江戸時代の完全市場市場の様子をリアクティブプログラミングを用いて、シミュレーションしてみるのは面白そうである。
屋号(正確には、株の譲渡によってお店が継がれていたので株がよいと思われるが馴染みやすい言葉を使うと屋号でよいと思う)を振舞いにして、お店の栄枯盛衰を表すのが面白いと思われる。
山室の本でも紹介されているが、1851年に諸問屋が再興されて以来、明治になるまでの諸問屋と商工組合の名簿が『諸問屋名前帳』に記されている(江戸時代、株を所有していないと商いができない業種が多かった。しかし、その制度が水野忠邦により1941年から2年にかけて一時廃された。これは、今日の規制緩和に相当する。しかし、彼が失脚すると1951年に再興される。これは、過当競争になるのを防ぐために規制の強化を再度した。これにより、株の所有者を公儀に届出る必要が生じた。この届出に基づいて新たに名簿が作成され、今日までこの記録が残った)。これは、国立国会図書館デジタルコレクションでインターネットで閲覧できる。例えば、このようになっている。

この部分は、舂米屋に関する情報で、三番組・四番組に属するコマからとってきたものである。一ページごとに問屋の場所と名前とその所有者が記載されている。また、所有者が変わった場合にはその情報も載っている。例えば、右側がそうである。ここでは、所有者が山鹿屋から田村屋に代わったことを示している。また、その事由も中ほどに小さい字で記載されている。
2.1 所有者の異動
それでは、所有者の異動が分かるようにしよう。諸問屋名前帳には、その事由が書かれているので、これを用いる。事由には、株を公儀から発行してもらい新規に開店した(Founding)、血縁家族に相続した(Inherited)、血縁家族に以外に譲渡した(Transferred)、店を閉じた(Closed)、店を閉じた後で店を引受けたい人が見つかった(TakenOver)の5つの形態がある。これを、新たなデータ型として次のように用意しよう。
data Owner = Founding | Inherited | Transferred | Closed | TakenOver deriving (Eq, Show, Read)
また、事由が発生した年を新たなデータ型Timeとして次のように定義しよう。
type Time = Int
発生した年と事由の対(Time, Owner)をイベントとすると、ある屋号で生じた所有者の変化はイベントの列で表すことができる(但し、年代順に並んでいるとする)。例えば、次のようになる。
kagaya :: [(Time, Owner)] kagaya = [(1732, Founding),(1740,Transferred),(1751,Inherited),(1762,Closed),(1780,TakenOver)]
上の例は、加賀屋の例であるが、1732年に店が新規に開設され、1740年に譲渡され、1751年に相続され、1762年に休業となり、1780年に引受となっている。今、任意の年での所有者がどのようにして店を得たのかを知るための関数situationを次のように用意したとする。
situation :: [(Time, Owner)] -> Time -> Maybe Owner situation es t = case takeWhile (\(t', _) -> t' < t) es of [] -> Nothing xs -> Just $ snd (last xs)
なお、takeWhile :: (a -> Bool) -> [a] -> [a] は述語(a -> Bool)をリスト[a]に適応して、次に述べるような述語を満たすリストを得る。これは、元々のリストの先頭の部分でかつそれらの要素はすべて述語を満たしているようなリストの中で最大の長さのものである(先頭の要素が述語を満たさない場合には空のリストとなる)。takeWhileの例:
*Main> takeWhile (<4) [1..10] [1,2,3] *Main> takeWhile (>2) [1..10] []
関数situationへの入力は、店の名前、調査したい年とする。例えば、加賀屋の状況を年代を追って調べると次のようになる。
*Main> situation kagaya 1700 Nothing *Main> situation kagaya 1733 Just Founding *Main> situation kagaya 1742 Just Transferred *Main> situation kagaya 1750 Just Transferred *Main> situation kagaya 1755 Just Inherited *Main> situation kagaya 1765 Just Closed *Main> situation kagaya 1770 Just Closed *Main> situation kagaya 1780 Just Closed *Main> situation kagaya 1785 Just TakenOver
上記のプログラムで、Just XXは、店がだれかによって所有されているときに現れ、このとき、XXという事由で所有者が店を得たことを示す。また、Nothingは、店がだれによっても所有されていないとき、即ち、開設前の状態の時に現れる。
ここでは、便利を優先して屋号で所有者の異動を示したが、実際に、移動したのは屋号ではなく株である。山室によれば、株の移動事由は、新規16%、相続9%、譲渡49%、休業23%、休業跡引受3%の割合であった。江戸時代は血縁での相続が当然だろうと思っていたが、事実はそうではなかったことが分かる。
また、店の存続年数もとても短く、15.7年であった。江戸時代は、店を開いてのんびりと暮らせるという状況ではなかったようだ。しかし、例外もある。朝ドラの「あさが来た」の主人公あさの生家である越後屋八郎兵衛(三井)は存続年数が171年である。越後屋は江戸時代を代表する商家であろうが、典型的な商店と思うと江戸の町人たちの真の姿を捉えることはできない。三井は際立って特殊な町人である。
2.2 御用金
江戸時代には、幕府の財政が窮迫したり、旧に多額の経費が必要になった時、町人から、御用金という名前で寄付を求めた。御用金は寄付なので、ぎりぎりの生活であれば御用金は出さないであろうし、利益が潤沢であればたくさんの御用金を拠出(山室の本では醵出となっている)するであろうという推定のもとに、店舗の繁盛の度合いを求めている。これによれば、都心型で日本橋地区で営業している店舗が一番御用金を納めているという結果を得ている。
さて、御用金を拠出する行為をイベントとし、その中で、高額のものを抜き出すことを考える。御用金は次のように定義しよう(単位は両で端数はなし)。
type Goyokin = Int
また、時間は御用金の募集開始時点から経過した時間とする。
type Time = Int
御用金拠出のイベントは拠出時間と御用金高とする。そこで、集まった御用金はイベントの列となるので、collectedMoneyとすると、例えば次のようになる。
collectedMoney :: [(Time, Goyokin)] collectedMoney = [(1,100),(2,1),(3,2),(5,20),(7,15),(9,1),(10,1),(13,25),(15,31)]
それでは、ある額以上の御用金のリスト求めることにする。そこで、次の関数filterEを定義する。
filterE :: (Goyokin -> Bool) -> [(Time, Goyokin)] -> [(Time, Goyokin)] filterE p es = [(time, goyokin) | (time, goyokin) <- es, p goyokin]
これを用いて、5両、10両、25両を越える御用金の拠出を求めると次のようになる。
*Main> filterE (>5) collectedMoney [(1,100),(5,20),(7,15),(13,25),(15,31)] *Main> filterE (>10) collectedMoney [(1,100),(5,20),(7,15),(13,25),(15,31)] *Main> filterE (>25) collectedMoney [(1,100),(15,31)]
filterEは少ない場合も求めることができる。例えば、25両より少ない拠出は次のように求めることができる。
*Main> filterE (<25) collectedMoney [(2,1),(3,2),(5,20),(7,15),(9,1),(10,1)]
2.3 御用金の累計
御用金はいくら集まったかが重要なので、ここでは、御用金のある時点での累計を求められるようにする。
そこで、御用金が拠出された時のイベントを拠出額を使うのではなく、次のように拠出額を加えるという関数に変更しよう。
collectedMoney :: [(Time, Goyokin -> Goyokin)] collectedMoney = [(1,(+100)),(2,(+1)),(3,(+2)),(5,(+20)),(7,(+15)),(9,(+1)),(10,(+1)),(13,(+25)),(15,(+31))]
上のプログラムで、(+100),(+1)はそれぞれ、100両加える、1両加えるという関数である。
次に、新たな御用金の拠出があった時、その時点までの拠出された御用金の総額をイベントとする関数accumulatedEを定義する。
accumulatedE :: Goyokin -> [(Time, Goyokin -> Goyokin)] -> [(Time, Goyokin)] accumulatedE x [] = [] accumulatedE x ((time, f) : es) = (time, f x) : accumulatedE (f x) es
これの実行結果は次のようになる。
*Main> accumulatedE 0 collectedMoney [(1,100),(2,101),(3,103),(5,123),(7,138),(9,139),(10,140),(13,165),(15,196)]
そしてある時点より以前に集まった御用金の総額を求める関数は、前に出てきた関数situationの中の型引数OwnerをGoyokinに替えればよいので、次のようにする。
situation' :: [(Time, Goyokin)] -> Time -> Maybe Goyokin situation' es t = case takeWhile (\(t', _) -> t' < t) es of [] -> Nothing xs -> Just $ snd (last xs)
これの実行結果を見ると次のようになる。
*Main> situation' (accumulatedE 0 collectedMoney) 0 Nothing *Main> situation' (accumulatedE 0 collectedMoney) 1 Nothing *Main> situation' (accumulatedE 0 collectedMoney) 2 Just 100 *Main> situation' (accumulatedE 0 collectedMoney) 3 Just 101 *Main> situation' (accumulatedE 0 collectedMoney) 4 Just 103 *Main> situation' (accumulatedE 0 collectedMoney) 5 Just 103 *Main> situation' (accumulatedE 0 collectedMoney) 6 Just 123 *Main> situation' (accumulatedE 0 collectedMoney) 7 Just 123 *Main> situation' (accumulatedE 0 collectedMoney) 8 Just 138 *Main> situation' (accumulatedE 0 collectedMoney) 9 Just 138 *Main> situation' (accumulatedE 0 collectedMoney) 10 Just 139 *Main> situation' (accumulatedE 0 collectedMoney) 11 Just 140 *Main> situation' (accumulatedE 0 collectedMoney) 12 Just 140
誰も拠出していない頃は、0ではなくnothingと出力される。また、時間1の時に1両の供出があるが、situation'で時間1より以前の総額を求めているがこの時間のものを含まないのでnothingである。