あるグループで雑談しているときに、インド人は2桁の掛け算ができるらしいということが話題になった。その時、「私もできるかもしれない。」という人が現れた。「お買い物計算を利用すればよいのよ。」ということだった。「試しにやってみましょうか?」ということで、「$47 \times 44$を計算してみるわね。」と言われた。「計算が終わるまで静かにしててね。」と言われたので、待っていた。どうも混乱されたようで、「$48 \times 42$でやってみる。」と言われたので、「ルールを変えるの。」と茶々を入れながらも、お願いということになった。しばらくして、2016と言った。隣の人は電卓をたたいてすでに答えを出していたので、正解であることが分かった。
この原理はどのようになっているのだろう。多くの人は一桁目が5である二けたの数を二乗する方法を知っているだろう。これは、二桁目の数とそれに1を加えたものを掛け算しその後に25をつければよい。例えば、$25^{2} = 2 \times 3 \times 100 + 25=625$である。
先ほどの計算もこれと同じ原理を用いているように思える。用いた数字にからくりがあるようにも思える。再提案された数字を見ると、一桁目の数字は2と8で、足し算すると10になる。先の一桁目の数が5も同じで足すと10になる。そこで一桁目が10の補数同士で二桁目が同じ数であるとき、その乗算は次のようにして得られそうである。「二桁目の数に対してそれとそれに1加えたものを乗算し、それに一桁目同士を乗算したものをくっつければよい」。
確認することとしよう。二桁目の数を$x$、一桁目の数を$a$とすると、この数を$x \times 10 + a \ \ (1 \leq x,a \leq 9 )$となる。そして、一桁目が補数となる数は$x \times 10 + (10- a)$となる。これらの乗算は次のようになる。
\begin{eqnarray}
&& (x \times 10 + (10-a)) \times (x \times 10 + a) \\
& = & (x \times 10 + (10-a)) \times (x \times 10)+ (x \times 10 + (10-a)) \times a \nonumber \\
& = & ( (x+1) \times 10 -a) \times (x \times 10)+ (x \times 10 + (10-a)) \times a \nonumber \\
& = & (x+1) \times x \times 100 - a \times x \times 10 + a \times x \times 10 + (10-a) \times a \nonumber \\
& = & (x+1) \times x \times 100 + (10-a) \times a
\end{eqnarray}
これで証明ができた。また、先の$48 \times 42$では、$x=4, a = 2 \ or \ 8$である。
しかし、この計算をした方はみんなに静寂を求めた後に、しばらく、頭の中で考えていた。もし、この原理が分かっていたならば、すぐさま、答えを出したはずである。これとは別の方法で答えを求めたようである。計算をする前に「お買い物計算」と言っていたので、もっと、別の方法があるのだろう。そこで、この計算をされた方の頭の中を想像することとしよう。
具体的な例として、キャンディーが袋詰めにされているとしよう。この例では、袋は42袋、それぞれの袋には48個のキャンディが入っていたことになる。そして、全部でいくつのキャンディがあるでしょうという問題になる。そこで、簡単に計算できるように、2袋を別にして、そこから残りの40袋に切りのいい数になるようにキャンディを移していくことにしよう。この場合には、別にした袋のそれぞれから一つずつ取り出して、40袋のそれぞれに移し、それぞれ50個のキャンディが納まるようにする。
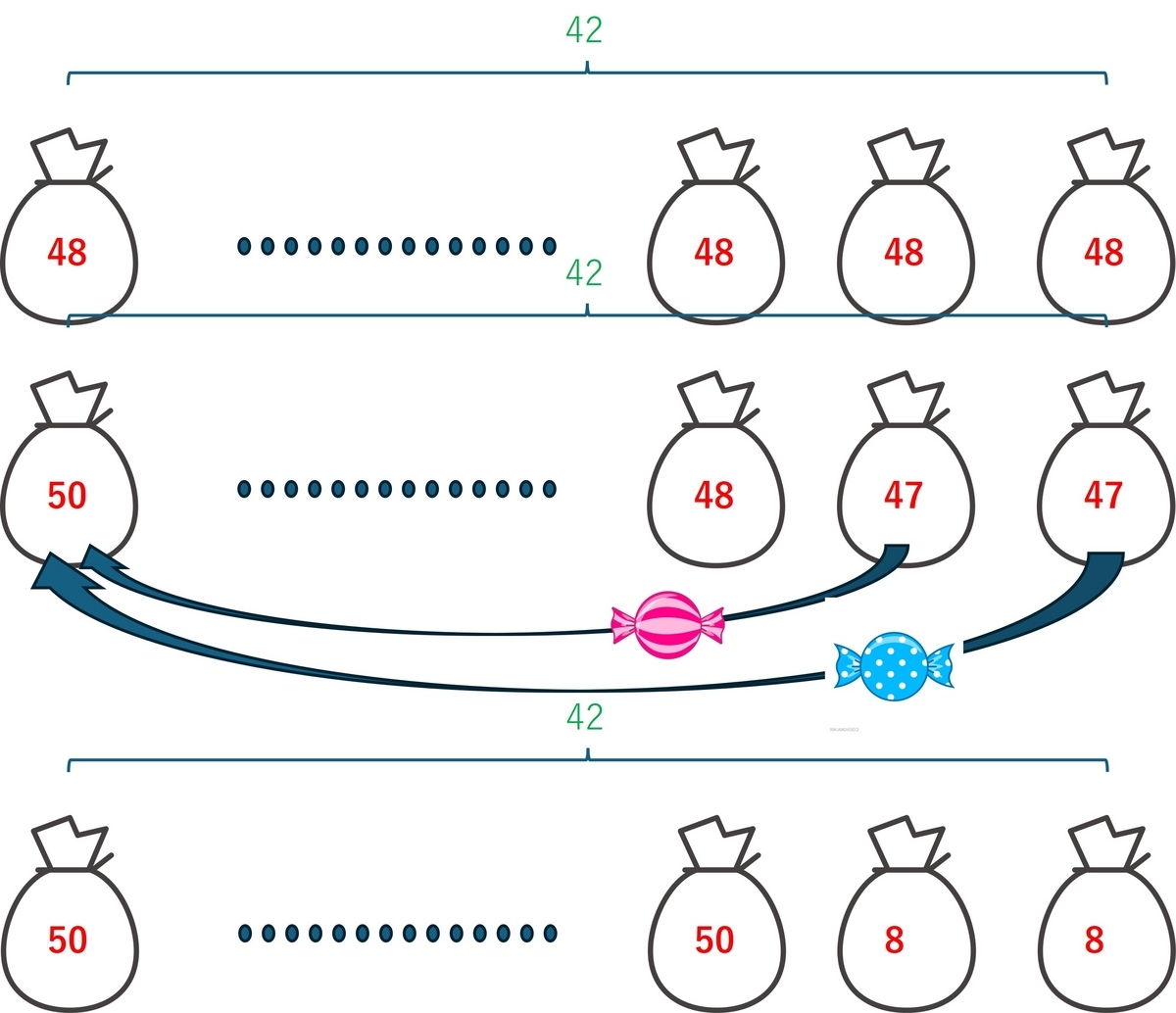
最終結果はどうだろう。50個のキャンディが詰まった袋が40袋と、8個のキャンディが取り残された袋が2袋となる。こうなると計算はとても簡単で$50 \times 40 + 8 \times 2 $となる。
それでは途中でやめられた$47 \times 44$はどうであろう。同じように下図のように求めればよい。
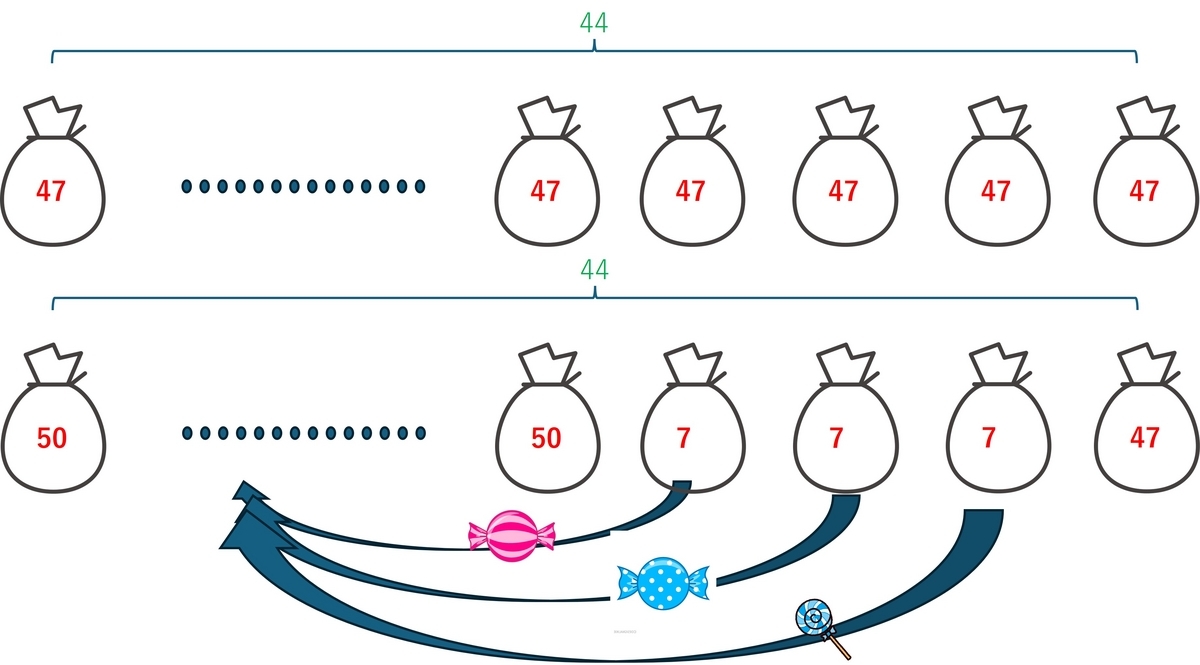
その結果は、$47 \times 44 = 50 \times 40 + 7 \times 3 + 47=2068 $となる。多くの人がいる前では、この図が出てくる前に混乱してしまったのだろう。
本当のところはこのように計算されていたのかはわからない。お買い物計算というヒントをもらって、袋を詰め替えることを私が考えただけなので、実際はもっと異なる良い方法があるのかもしれない。現在は電卓があるので、ある問題を別の問題にして単純に解くための工夫をする必要がなくなった。しかし、コンピュータが出現する前の人々にはこのような生活の知恵はたくさんあったのだろう。頭の体操には時々このようなことを考えるのも良いことである。